题目内容
已知函数f(x)＝
(1)判断f(x)的奇偶性；
(2)判断f(x)的单调性，并加以证明；
(3)写出f(x)的值域．
[解析] (1)f(x)＝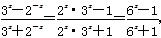
，
所以f(－x)＝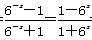
＝－f(x)，x∈R，
则f(x)是奇函数．
(2)f(x)＝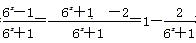
在R上是增函数．
证明如下：任意取x1，x2，使得x1>x2，
∵6x1>6x2>0，
则f(x1)－f(x2)＝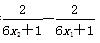
＝
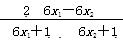>0，
所以f(x1)>f(x2)，则f(x)在R上是增函数．
(3)∵0<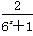
<2，
∴f(x)＝1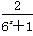－∈(－1,1)，
则f(x)的值域为(－1,1)．
练习册系列答案
相关题目
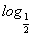(x2－ax＋3a)在区间[2，＋∞)上是减函数，则实数a的取值范围是( )
＋21＋log23；
，cosx－cosy＝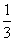
D.
＝3，则△ABC面积的最大值为( )
B.
D．3