题目内容
函数f(x)＝x3－2x2＋2x的零点个数为( )
A．0 B．1
C．2 D．3
B
[解析]∵f(x)＝x3－2x2＋2x＝x(x2－2x＋2)，
若x2－2x＋2＝0，Δ＝4－8<0，
∴x2－2x＋2≠0，
∴f(x)的零点只有1个，故选B.
练习册系列答案
名校课堂系列答案
相关题目
某公司今年1月份推出新产品A，其成本价为492元/件，经试销调查，销售量与销售价的关系如下表：
| 销售价x(元/件) | 650 | 662 | 720 | 800 |
| 销售量y(件) | 350 | 333 | 281 | 200 |
由此可知，销售量y(件)与销售价x(元/件)可近似看作一次函数y＝kx＋b的关系(通常取表中相距较远的两组数据所得的一次函数较为精确)．
试问：销售价定为多少时，1月份利润最大？并求最大利润和此时的销售量．
，＋∞)．
)＝
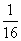，则sin(2α＋
)的值为________．
，且
＝－27.