Question

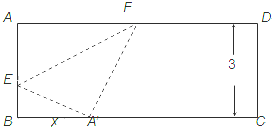
如图，将一条宽为3的矩形长条纸带一角折起，使顶点A落在BC边上（落点为A′）．设△A′BE的面积为y，BA′=x，则函数y=f（x）的表达式为（写出定义域）

 

．

Answer 1

考点：函数解析式的求解及常用方法

专题：函数的性质及应用

分析：可设BE=m，则AE=3-m，由△ABE是直角三角形，由勾股定理可得m=

9-x2

6

，再由三角形面积公式得y=f（x）的解析式．

解答： 解：设BE=m，则AE=3-m，由△ABE是直角三角形，由勾股定理可得m²+x²=（3-m）²，
解得m=

9-x2

6

，∴由三角形面积公式得y=f（x）=

1

2

•x•

9-x2

6

，
即f（x）=-

1

12

x³+

3

4

x，
又由0＜m＜3得0＜

9-x2

6

＜3即0＜x＜3，
故答案为：f(x)=-

1

12

x3+

3

4

x（0＜x＜3）．

点评：考查函数解析式的求解方法，利用折叠前后量的变化关系，建立等量关系是解决本题的关键．