题目内容
求函数y=x2+x(-1≤x≤3)的值域.
考点:二次函数的性质
专题:函数的性质及应用
分析:由题意可得函数在[-1,-
]单调递减,[-
,3]单调递减,结合对称性可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:配方可得y=x2+x=(x+
)2-
,
可知该二次函数的图象为开口向上的抛物线,对称轴为x=
,
∴函数在[-1,-
]单调递减,[-
,3]单调递减,
∴当x=-
时,y取最小值-
,
当x=3时,y取最大值12,
∴函数的值域为:[-
,12]
故答案为::[-
,12]
| 1 |
| 2 |
| 1 |
| 4 |
可知该二次函数的图象为开口向上的抛物线,对称轴为x=
| 1 |
| 2 |
∴函数在[-1,-
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=-
| 1 |
| 2 |
| 1 |
| 4 |
当x=3时,y取最大值12,
∴函数的值域为:[-
| 1 |
| 4 |
故答案为::[-
| 1 |
| 4 |
点评:本题考查二次函数区间的最值,属基础题.

练习册系列答案
相关题目
在映射f:A→B中,A=B={(x,y)|x,y∈R},且f:(x,y)→(x-y,x+y),则与B中的元素(-1,1)对应的A中的元素为( )
| A、(0,1) |
| B、(1,3) |
| C、(-1,-3) |
| D、(-2,0) |
 如图,AD⊥CD,AC⊥BC,AB=4,AD=CD=2,M为线段AB的中点,平面ACD⊥平面ABC.
如图,AD⊥CD,AC⊥BC,AB=4,AD=CD=2,M为线段AB的中点,平面ACD⊥平面ABC.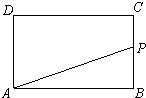 如图,在长为4、宽为2的矩形ABCD上有一点P,沿折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).
如图,在长为4、宽为2的矩形ABCD上有一点P,沿折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).