题目内容
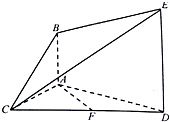如图所示，AB∥平面ACD，DE∥AB，△ACD是正三角形，F是CD的中点，AD=4，DE=2AB=3．（1）求证：AF∥平面BCE；
（2）求四棱锥C-ABED的体积．
考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题：计算题,证明题,空间位置关系与距离
分析：（1）取CE的中点G，连结BG，GF，由线面平行的判定定理证明AF∥平面BCE；（2）取AD的中点H，连接CH，从而CH⊥AD，求体积．
解答：
解：（1）
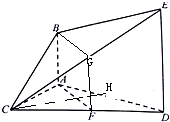
如图，取CE的中点G，连结BG，GF，
∵F是CD的中点，
∴GF∥ED∥BA且GF=
ED=AB
∴BG∥AF，又BG?平面BCE
∴AF∥平面BCE．
（2）取AD的中点H，连接CH，则CH⊥AD，
又BA⊥面ACD
∴BA⊥CH
∴CH⊥面ABED
∴V=
CH×S梯形ABED=
×2
×
×(
+3)×4=6
．
如图，取CE的中点G，连结BG，GF，
∵F是CD的中点，
∴GF∥ED∥BA且GF=
| 1 |
| 2 |
∴BG∥AF，又BG?平面BCE
∴AF∥平面BCE．
（2）取AD的中点H，连接CH，则CH⊥AD，
又BA⊥面ACD
∴BA⊥CH
∴CH⊥面ABED
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
点评：本题综合考查了线面平行的判定与体积公式，属于中档题．
练习册系列答案
小学期末标准试卷系列答案
相关题目
已知集合U=R，集合A={x|y=
}，则∁UA=（ ）
1-
|
| A、{x|x＜0或x≥1} |
| B、{x|0≤x＜1} |
| C、{x|x≥1} |
| D、{x|x＜0} |
函数y=f（x）的图象经过点（2，1），则y=f（x+3）的反函数的图象必过定点（ ）
| A、（1，2） |
| B、（2，-1） |
| C、（1，-1） |
| D、（2，-2） |
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1．