题目内容
已知集合U=R，集合A={x|y=
}，则∁UA=（ ）
1-
|
| A、{x|x＜0或x≥1} |
| B、{x|0≤x＜1} |
| C、{x|x≥1} |
| D、{x|x＜0} |
考点：补集及其运算
专题：集合
分析：先由被开方数大于或等于零，得到一个关于x的分式不等式，从而将集合A化简，再进行补集运算．
解答：
解：在集合A中，由1-
≥0，得
≥0，
从而x≥1，或x＜0，
由U=R知，∁UA={x|0≤x＜1}．
故选B．
| 1 |
| x |
| x-1 |
| x |
从而x≥1，或x＜0，
由U=R知，∁UA={x|0≤x＜1}．
故选B．
点评：本题属容易题，但容易出错，考查了根式的性质、分式不等式的解法及补集运算法则，特别注意式子中等号成立的情况．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在正方体ABCD-A1B1C1D1中，M是正方形ABCD的中心，N是棱CC1（包括端点）上的动点，现给出以下命题：
从一个棱长为3的正方体中切去一些部分，得到一个几何体，其三视图如图，则该几何体的体积是（ ）| A、3 | B、7 | C、9 | D、18 |
若函数f（x）=-a•2x与f（x）=4x+a+1的图象有交点，则a的取值范围是（ ）
A、a≤2-2
| ||||
| B、a＜-1 | ||||
C、-1≤a≤2-2
| ||||
D、a≤2-2
|
sin240°等于（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知定义在R上的函数f（x）满足f（1）=1，且f（x）的导数f′（x）在R上恒有f′（x）＜
，则不等式f（x）＜
x+
的解集为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、（1，+∞） |
| B、（-∞，-1） |
| C、（-1，1） |
| D、（-∞，-1）∪（1，+∞） |
函数y=lg（6+x-x2）的定义域是（ ）
| A、{x|x＜-2，或x＞3} |
| B、{x|-2＜x＜3} |
| C、{x|2＜x＜3} |
| D、R |
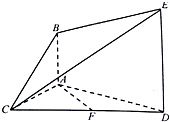如图所示，AB∥平面ACD，DE∥AB，△ACD是正三角形，F是CD的中点，AD=4，DE=2AB=3．