题目内容
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1．（Ⅰ）证明：PC⊥AD；
（Ⅱ）求二面角A-PC-D的正弦值；
（Ⅲ）求三棱锥P-ACD外接球的体积．
考点：棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系,二面角的平面角及求法
专题：证明题,空间位置关系与距离
分析：（1）先证明DA⊥平面PAC，从而推出DA⊥PC；（2）过A作AM⊥PC交PC于点M，连接DM，则∠AMD为所求角；（3）长方体的对角线为球的直径．
解答：
解：（Ⅰ）∵PA⊥平面ABCD，∴DA⊥PA
又∵AC⊥AD，∴DA⊥平面PAC
∴DA⊥PC．
（Ⅱ）过A作AM⊥PC交PC于点M，连接DM，则∠AMD为所求角．
在Rt△PAC中，AM=
=
，
在Rt△DAM中，DM=
=
=
，
在Rt△AMD中，sin∠AMD=
=
．
（Ⅲ）求三棱锥P-ACD外接球即为以AP，AD，AC为棱的长方体的外接球，
长方体的对角线为球的直径；
∵l2=22+22+12=9=（2R）2
∴R=
；
∴V=
πR3=
π×(
)3=
π．
又∵AC⊥AD，∴DA⊥平面PAC
∴DA⊥PC．
（Ⅱ）过A作AM⊥PC交PC于点M，连接DM，则∠AMD为所求角．
在Rt△PAC中，AM=
| 2 | ||
|
| 2 | ||
|
在Rt△DAM中，DM=
| DA2+AM2 |
22+(
|
2
| ||
| 5 |
在Rt△AMD中，sin∠AMD=
| AD |
| DM |
| ||
| 6 |
（Ⅲ）求三棱锥P-ACD外接球即为以AP，AD，AC为棱的长方体的外接球，
长方体的对角线为球的直径；
∵l2=22+22+12=9=（2R）2
∴R=
| 3 |
| 2 |
∴V=
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 9 |
| 2 |
点评：本题考查了线面垂直，线线垂直的证明，及二面角的平面角的作法，同时考查了外接球与内几何体的等量关系，综合性较强．
练习册系列答案
相关题目
函数y=lg（6+x-x2）的定义域是（ ）
| A、{x|x＜-2，或x＞3} |
| B、{x|-2＜x＜3} |
| C、{x|2＜x＜3} |
| D、R |
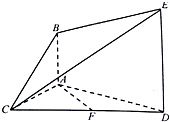如图所示，AB∥平面ACD，DE∥AB，△ACD是正三角形，F是CD的中点，AD=4，DE=2AB=3．