题目内容
函数y=f（x）的图象经过点（2，1），则y=f（x+3）的反函数的图象必过定点（ ）
| A、（1，2） |
| B、（2，-1） |
| C、（1，-1） |
| D、（2，-2） |
考点：反函数
专题：函数的性质及应用
分析：由已知得y=f（x+3）的图象经过点（-1，1），从而y=f（x+3）的反函数的图象必过定点（1，-1）．
解答：
解：∵函数y=f（x）的图象经过点（2，1），
∴y=f（x+3）的图象经过点（-1，1），
∴y=f（x+3）的反函数的图象必过定点（1，-1）．
故选：C．
∴y=f（x+3）的图象经过点（-1，1），
∴y=f（x+3）的反函数的图象必过定点（1，-1）．
故选：C．
点评：本题考查反函数的性质的合理运用，是基础题，解题时要认真审题．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
如图所示，在正方体ABCD-A1B1C1D1中，M是正方形ABCD的中心，N是棱CC1（包括端点）上的动点，现给出以下命题：已知定义在R上的函数f（x）满足f（1）=1，且f（x）的导数f′（x）在R上恒有f′（x）＜
，则不等式f（x）＜
x+
的解集为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、（1，+∞） |
| B、（-∞，-1） |
| C、（-1，1） |
| D、（-∞，-1）∪（1，+∞） |
函数y=lg（6+x-x2）的定义域是（ ）
| A、{x|x＜-2，或x＞3} |
| B、{x|-2＜x＜3} |
| C、{x|2＜x＜3} |
| D、R |
已知椭圆C：
+
=1（b＞0）的左、右焦点分别为F1，F2，直线AB过右焦点F2，和椭圆C交于A，B两点，且满足
=2
，∠F1AB=90°，则椭圆C的离心率为（ ）
| x2 |
| 3 |
| y2 |
| b2 |
| AF1 |
| F2B |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某地固定电话市话收费规定：前三分钟0.20元（不满三分钟按三分钟计算），以后每加一分钟增收0.10元 （不满一分钟按一分钟计算），那么某人打市话550秒，应支付电话费（ ）
| A、1.00元 |
| B、0.90元 |
| C、1.20元 |
| D、0.80元 |
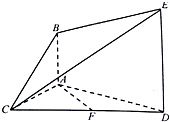如图所示，AB∥平面ACD，DE∥AB，△ACD是正三角形，F是CD的中点，AD=4，DE=2AB=3．