题目内容
已知A（-2，2），B（-3，-1），试在直线l：2x-y-1=0上求一点P，使得|PA|2+|PB|2最小．
考点：两点间距离公式的应用
专题：计算题,直线与圆
分析：设P（x，2x-1），利用距离公式，结合配方法，即可得出结论．
解答：
解：设P（x，2x-1），则
∵A（-2，2），B（-3，-1），
∴|PA|2+|PB|2=（x+2）2+（2x-3）2+（x+3）2+4x2=10x2-2x+22=10（x-
）2+
，
∴x=
时，|PA|2+|PB|2最小，
此时P（0.1，-0.8）．
∵A（-2，2），B（-3，-1），
∴|PA|2+|PB|2=（x+2）2+（2x-3）2+（x+3）2+4x2=10x2-2x+22=10（x-
| 1 |
| 10 |
| 219 |
| 10 |
∴x=
| 1 |
| 10 |
此时P（0.1，-0.8）．
点评：本题考查两点间距离公式的应用，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
从一个棱长为3的正方体中切去一些部分，得到一个几何体，其三视图如图，则该几何体的体积是（ ）| A、3 | B、7 | C、9 | D、18 |
函数y=lg（6+x-x2）的定义域是（ ）
| A、{x|x＜-2，或x＞3} |
| B、{x|-2＜x＜3} |
| C、{x|2＜x＜3} |
| D、R |
某地固定电话市话收费规定：前三分钟0.20元（不满三分钟按三分钟计算），以后每加一分钟增收0.10元 （不满一分钟按一分钟计算），那么某人打市话550秒，应支付电话费（ ）
| A、1.00元 |
| B、0.90元 |
| C、1.20元 |
| D、0.80元 |
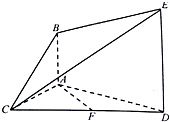如图所示，AB∥平面ACD，DE∥AB，△ACD是正三角形，F是CD的中点，AD=4，DE=2AB=3．