题目内容
先后抛掷两颗骰子,则所得点数之和为7的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:由题意知本题是一个古典概型,试验发生包含的事件是抛掷两颗骰子,共有6×6种结果,满足条件的事件是点数之和是7,可以列举出所有的事件,共有6种结果,得到概率.
解答:
解:由题意知本题是一个古典概型,
试验发生包含的事件是抛掷两颗骰子,共有6×6=36种结果,
满足条件的事件是点数之和是7,可以列举出所有的事件
(1,6)(2,5)(3,4)(4,3)(5,2)(6,1),共有6种结果,
根据古典概型概率公式得到P=
=
,
故选:C
试验发生包含的事件是抛掷两颗骰子,共有6×6=36种结果,
满足条件的事件是点数之和是7,可以列举出所有的事件
(1,6)(2,5)(3,4)(4,3)(5,2)(6,1),共有6种结果,
根据古典概型概率公式得到P=
| 6 |
| 36 |
| 1 |
| 6 |
故选:C
点评:本题考查古典概型,是一个典型的古典概型问题,本题可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是大纲对这一部分的要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=2x-
-m的一个零点在区间(1,3)内,则实数m的取值范围是( )
| 3 |
| x |
| A、(-1,7) |
| B、(0,5) |
| C、(-7,1) |
| D、(1,5) |
已知定义在(-1,1)上的函数f (x),其导函数为f′(x)=l+cosx,且f(0)=0,如果f(1-x)+f(l-x2)<0,则实数x的取值范围为( )
| A、(0,1) | ||||
B、(1,
| ||||
C、(-2,-
| ||||
D、(1,
|
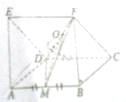 如图,在直三棱柱ADE-BCF中,面ABFE和面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运动向量方法证明:
如图,在直三棱柱ADE-BCF中,面ABFE和面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运动向量方法证明: 已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.