题目内容

直线
3
x+y-2=0与圆x2+y2=4交于A，B两点，则|AB|=（　　）
A、1
B、2
3
C、2
2
D、2
考点：直线与圆相交的性质
专题：直线与圆
分析：由条件利用直线和圆相交的性质，点到直线的距离公式，弦长公式，求得|AB|的值．
解答： 解：由于圆的半径为2，弦心距d=
|0+0-2|
3+1
=1，可得弦长AB=2
r2-d2
=2
3
，
故选：B．
点评：本题主要考查直线和圆相交的性质，点到直线的距离公式，弦长公式的应用，属于基础题．
练习册系列答案
相关题目
某地方政府在某地建一座桥，两端的桥墩相距m米，此工程只需建两端桥墩之间的桥面和桥墩（包括两端的桥墩），经预测，一个桥墩的费用为32万元，相邻两个桥墩之间的距离均为x，且相邻两个桥墩之间的桥面工程费用为（1+x）x万元，假设所有桥墩都视为点且不考虑其它因素，记工程总费用为y万元．
（1）试写出y关于x的函数关系式；
（2）当m=80米时，需要新建多少个桥墩才能使y最小？
已知函数f （x）=ax-ex（a∈R），g（x）=
1nx
x
．
（I）求函数f （x）的单调区间；
（Ⅱ）?x0∈（0，+∞），使不等式f （x）≤g（x）-ex成立，求a的取值范围．
下列各组函数f（x）与g（x）的图象相同的是（　　）
A、f（x）=x，g（x）=（
x
）2
B、f（x）=x2，g（x）=（x+1）2
C、f（x）=1，g（x）=x0
D、f（x）=|x|，g（x）=
x
-x
(x≥0)
(x＜0)
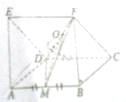如图，在直三棱柱ADE-BCF中，面ABFE和面ABCD都是正方形且互相垂直，M为AB的中点，O为DF的中点，运动向量方法证明：
（1）OM∥平面BCF；
（2）平面MDF⊥平面EFCD．
求证：
1
1+sin2x
+
1
1+cos2x
+
1
2+tan2x
+
1
2+cot2x
=2．
已知A（2，1），B（1，-2），C（
3
5
，-
1
5
），动点P（a，b）满足0≤
OP
•
OA
≤2且0≤
OP
•
OB
≤2，则点P到点C的距离大于
1
4
的概率为
 
．
已知方程x2-ax+2a=0的两个根均大于1，则实数a的取值范围为
 
．
已知函数y=Asin（ωx+φ）（A＞0，|φ|＜π）的一段图象如图所示．
（1）求函数的解析式；
（2）求这个函数的单调递增区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网