题目内容
3.若函数f(x)=ax3-bx+2,当x=1时,函数f(x)取极值0.(1)求函数f(x)的解析式;
(2)若关于x的方程f(x)=k有三个零点,求实数k的取值范围.
分析 (1)求出函数的导数,利用函数的极值点以及极值,求解a,b即可.
(2)求出函数的极值点判断函数的单调性,推出函数的极值,然后求解k的范围.
解答 解 (1)由题意可知f′(x)=3ax2-b.
$\left\{\begin{array}{l}f(1)=0\\ f'(1)=0\end{array}\right.⇒\left\{\begin{array}{l}a=1\\ b=3\end{array}\right.$
故所求的函数解析式为f(x)=x3-3x+2.
(2)由(1)可知f′(x)=3x2-3=3(x-1)(x+1).
令f′(x)=0得x=1或x=-1,
当x变化时,f′(x),f(x)的变化情况如下表所示:
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
当x=1时,f(x)有极小值0,
故实数k的取值范围为(0,4).
点评 本题考查函数的导数的综合应用,函数的极值以及单调性的判断,考查转化思想以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.向量$\overrightarrow a=({2,-1}),\overrightarrow b=({x,1})$,若$2\overrightarrow a+\overrightarrow b$与$\overrightarrow b$共线,则x=( )
| A. | 2 | B. | -2 | C. | $-2+\sqrt{5}$ | D. | $-2-\sqrt{5}$ |
14.抛掷两枚质地的骰子,得到的点数分别为a,b,那么直线bx+ay=1的斜率$k≥-\frac{2}{5}$的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |
11.下列判断错误的是( )
| A. | “am2<bm2”是“a<b”成立的充分不必要条件 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x0∈R,x03-x02-1>0” | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
10.在等比数列{an}中,设a2=3,a5=81,bn=log3an,则数列{bn}的前n项和Sn为( )
| A. | $\frac{{{n^2}-n}}{2}$ | B. | $\frac{n^2}{2}$ | C. | $\frac{{{n^2}+n}}{2}$ | D. | $\frac{{{n^2}+2n}}{2}$ |
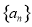 的前
的前 项和为
项和为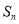 ,且
,且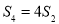 ,
,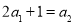 .
.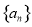 的通项公式;
的通项公式;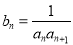 ,求
,求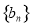 的前
的前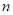 项和
项和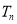 .
.