题目内容
(1)在等比数列{an}中,a5=162,公比q=3,前n项和Sn=242,求首项a1和项数n.
(2)数列{an}中,an=
(n∈N*),求数列{an}的前n项的和Sn.
(2)数列{an}中,an=
| 1 |
| (n+1)(n+3) |
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)由题意联立方程组即可求得结论;
(2)an=
=
(
-
),利用裂项法求和即得结论.
(2)an=
| 1 |
| (n+1)(n+3) |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+3 |
解答:
解:(1)由已知,得
,
解得a1=2,n=5.
(2)an=
=
(
-
)
∴sn=
(
-
+
-
+
-
+…+
-
)=
(
+
-
-
)=
(
-
),
∴sn=
-
.
|
解得a1=2,n=5.
(2)an=
| 1 |
| (n+1)(n+3) |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+3 |
∴sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| n+1 |
| 1 |
| n+3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2 |
| 5 |
| 6 |
| 2n+5 |
| (n+2)(n+3) |
∴sn=
| 5 |
| 12 |
| 2n+5 |
| 2(n+2)(n+3) |
点评:本题主要考查等比数列的通项公式及求和公式等知识,考查学生利用裂项相消法求数列的和的运用求解能力,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
过原点的直线交双曲线xy=
于P、Q两点,现将坐标平面沿x轴折成直二面角,则折后线段PQ的长度的最小值等于( )
| 2 |
| A、4 | ||
B、2
| ||
| C、2 | ||
D、
|
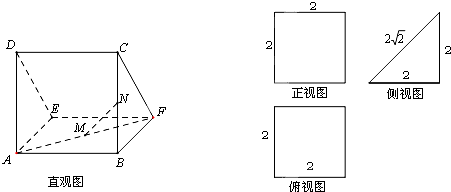
空间几何体的三视图如图所示,则该几何体的体积为( )


A、4+
| ||||
B、4π+2
| ||||
C、2π+
| ||||
D、2π+
|