题目内容
某房地产开发商投资81万元建一座写字楼,第一年维修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元.
(Ⅰ)若扣除投资和各种维修费,则从第几年开始获取纯利润?
(Ⅱ)若干年后开发商为了投资其他项目,有两种处理方案:①年平均利润最大时以47万元出售该楼; ②纯利润总和最大时,以10万元出售该楼,问哪种方案盈利更多?
(Ⅰ)若扣除投资和各种维修费,则从第几年开始获取纯利润?
(Ⅱ)若干年后开发商为了投资其他项目,有两种处理方案:①年平均利润最大时以47万元出售该楼; ②纯利润总和最大时,以10万元出售该楼,问哪种方案盈利更多?
考点:数列的应用
专题:应用题,等差数列与等比数列
分析:(Ⅰ)设第n年获取利润为y万元,n年共收入租金30n万元.付出装修费共n+
×2=n2,付出投资81万元,由此可知利润y=30n-(81+n2),由y>0能求出从第几年开始获取纯利润.
(Ⅱ)①利用基本不等式进行求解,②纯利润总和最大时,以10万元出售,利用二次函数的性质求出最大利润.
| n(n-1) |
| 2 |
(Ⅱ)①利用基本不等式进行求解,②纯利润总和最大时,以10万元出售,利用二次函数的性质求出最大利润.
解答:
解:(Ⅰ)设第n年获取利润为y万元
n年共收入租金30n万元,付出维修费构成一个以1为首项,2为公差的等差数列,
共n+
×2=n2
因此利润y=30n-(81+n2),------------(4分)
令y>0解得:3<n<27,
所以从第4年开始获取纯利润.------------(6分)
(Ⅱ)年平均利润W=
=30-
-n≤30-2
=12(当且仅当
=n,即n=9时取等号)
所以9年后共获利润:12×9+47=155(万元)------------(8分)
利润y=30n-(81+n2)=-(n-15)2+144
所以15年后共获利润:144+10=154 (万元)------------(10分)
方案①获利多且时间比较短,所以选择方案①.-------------(12分)
n年共收入租金30n万元,付出维修费构成一个以1为首项,2为公差的等差数列,
共n+
| n(n-1) |
| 2 |
因此利润y=30n-(81+n2),------------(4分)
令y>0解得:3<n<27,
所以从第4年开始获取纯利润.------------(6分)
(Ⅱ)年平均利润W=
| 30n-(81+n2) |
| n |
| 81 |
| n |
| 81 |
| 81 |
| n |
所以9年后共获利润:12×9+47=155(万元)------------(8分)
利润y=30n-(81+n2)=-(n-15)2+144
所以15年后共获利润:144+10=154 (万元)------------(10分)
方案①获利多且时间比较短,所以选择方案①.-------------(12分)
点评:本题考查数列的性质和应用,同时考查了利基本不等式求函数的最值,解题时要认真审题,仔细解答.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
函数f(x)=-x2+2(a-1)x+2在(-∞,4)上是增函数,则实数a的范围是( )
| A、a≤-3 | B、a≤5 |
| C、a≥3 | D、a≥5 |
在下列关于点P,直线l、m与平面α、β的命题中,正确的是( )
| A、若m⊥α,l⊥m,则l∥α |
| B、若α⊥β,α∩β=m,P∈α,P∈l,且l⊥m,则l⊥β |
| C、若l,m是异面直线,m?α,m∥β,l?β,l∥α,则α∥β |
| D、若α⊥β,且l⊥β,m⊥l,则m⊥α |
若不等式组
,表示的平面区域是一个钝角三角形,则实数k的取值范围为( )
|
| A、(0,1) |
| B、(-∞,-1)∪(0,1) |
| C、(-1,0)∪(1,+∞) |
| D、D(-1,0) |
符合下列条件的三角形有且只有一个的是( )
| A、a=1,b=2,c=3 | ||
| B、a=1,b=2,∠A=100° | ||
C、a=1,b=
| ||
| D、b=c=1,∠B=45° |
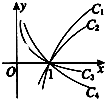 已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为
已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为