题目内容
已知抛物线y=2px2的焦点为F,点P(1,
)在抛物线上,过P作PQ垂直于抛物线的准线,垂足为Q,若抛物线的准线与对称轴相交于点M,则四边形PQMF的面积等于多少?
| 1 |
| 4 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先利用待定系数法求出抛物线方程,然后由题意求出四边形PQMF的面积.
解答:
解:因为抛物线y=2px2,点P(1,
)在抛物线上,
所以
=2p,即p=
,
所以抛物线方程为y=
x2即x2=4y;
所以F(0,1),Q(1,-1),M(0,-1),
所以四边形PQMF为梯形,它的面积等于
(PQ+FM)×MQ=
×
×1=
.
| 1 |
| 4 |
所以
| 1 |
| 4 |
| 1 |
| 8 |
所以抛物线方程为y=
| 1 |
| 4 |
所以F(0,1),Q(1,-1),M(0,-1),
所以四边形PQMF为梯形,它的面积等于
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 4 |
| 13 |
| 8 |
点评:本题考查了抛物线方程的求法以及抛物线性质的运用.

练习册系列答案
相关题目
已知不平行于坐标轴的直线l与以原点O为中心的双曲线
-
=1(a>0,b>0)的两 及其两条渐近线从左到右依次交于A,B,C,D不同的四点,则下列一定成立的是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、|AD|=2|BC| | ||||||||
| B、|AB|=|BC|=|CD| | ||||||||
C、
| ||||||||
D、
|
函数f(x)=
的图象关于( )对称.
| 1 |
| x |
| A、x轴 | B、y轴 | C、原点 | D、y=1 |
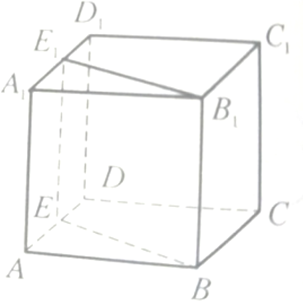 经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E.求证:BB1∥E1E.
经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E.求证:BB1∥E1E.