题目内容

已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）中
b
a
=2，则离心率e=
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：运用双曲线的a，b，c的关系：a2+b2=c2，及离心率公式e=
c
a
，即可计算得到．
解答： 解：由于
b
a
=2，
即b=2a，c=
a2+b2
=
a2+4a2

=
5
a，
则e=
c
a
=
5
．
故答案为：
5
．
点评：本题考查双曲线的性质：离心率，考查运算能力，属于基础题．
练习册系列答案
相关题目
复数 
(1+
3
i)2
3
i-1
的值是
 
．
已知直线2x-y+m=0与x2+y2=25的交点为M，N．求△MON的最大面积．
如图一，△ABC是正三角形，△ABD是等腰直角三角形，AB=BD=2．将△ABD沿边AB折起，使得△ABD与△ABC成30°的二面角D-AB-C，如图二，在二面角D-AB-C中．
（1）求D、C之间的距离；
（2）求CD与面ABC所成的角的大小；
（3）求证：对于AD上任意点H，CH不与面ABD垂直．
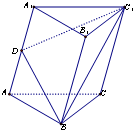如图，三棱柱ABC-A1B1C1中，D是棱AA1的中点，平面BDC1分此棱柱为上下两部分，则这上下两部分体积的比为（　　）
A、2：3B、1：1
C、3：2D、3：4
已知抛物线y=2px2的焦点为F，点P（1，
1
4
）在抛物线上，过P作PQ垂直于抛物线的准线，垂足为Q，若抛物线的准线与对称轴相交于点M，则四边形PQMF的面积等于多少？
对于函数f（x）及其定义域内的一个区间[m，n]（m＜n），若f（x）在[m，n]内的值域为[m，n]，则称[m，n]为f（x）的“保值区间”．
（1）求函数y=-x+6的一个“保值区间”；
（2）若函数y=（1+a）-
a2
x
的“保值区间”是[m，n]，求n-m的最大值；
（3）函数f（x）=ax2-2x的“保值区间”能否是[-1，2]？若能，求出a的一个值；若不能，说明理由；
（4）写出函数f（x）=x2-2x的一个“保值区间”；判断是否还有其它的“保值区间”（不必证明）．
已知矩形ABCD的顶点在半径为13的球O的球面上，且AB=8，BC=6，则棱锥O-ABCD的高为（　　）
A、12B、13C、14D、5
如果在某个区间内恒有f′（x）=0，那么函数f（x）有什么特性？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网