题目内容
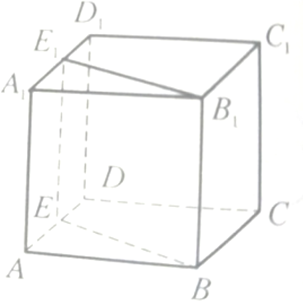经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E．求证：BB1∥E1E．考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：利用正方体的性质，只要证BB1∥平面ADD1A1，结合线面平行的性质可证．
解答：
证明：因为几何体为正方体，
所以BB1∥平面ADD1A1，
又BB1?平面BB1E1E，平面BB1E1E∩平面ADD1A=EE1，
所以BB1∥EE1．
所以BB1∥平面ADD1A1，
又BB1?平面BB1E1E，平面BB1E1E∩平面ADD1A=EE1，
所以BB1∥EE1．
点评：本题考查了正方体中的线线平行的判定，关键是正确利用正方体的性质得到BB1∥平面ADD1A1，再结合线面平行的性质定理可证．
练习册系列答案
相关题目
已知随机变量ξ～（100，
），则当P（ξ=k）取得最大值时，k的值为（ ）
| 1 |
| 2 |
| A、49 | B、50 |
| C、49或50 | D、50或51 |
已知θ为钝角，且sinθ=
，则tan
=（ ）
| ||
| 2 |
| θ |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
如图一，△ABC是正三角形，△ABD是等腰直角三角形，AB=BD=2．将△ABD沿边AB折起，使得△ABD与△ABC成30°的二面角D-AB-C，如图二，在二面角D-AB-C中．