题目内容
已知函数f(x)=alnx+
+x(a≠0).
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x-2y=0垂直,求实数a的值;
(2)讨论函数f(x)的单调性.
| 2a2 |
| x |
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x-2y=0垂直,求实数a的值;
(2)讨论函数f(x)的单调性.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的概念及应用
分析:(1)先求导函数,然后根据曲线y=f(x)在点(1,f(1))处的切线与直线x-2y=0垂直则f′(1)=-2,从而可求出a的值;
(2)确定函数的定义域,求导函数,利用导数的正负,分类讨论,即可求得函数f(x)的单调性.
(2)确定函数的定义域,求导函数,利用导数的正负,分类讨论,即可求得函数f(x)的单调性.
解答:
解:(1)f(x)的定义域为{x|x>0},f′(x)=
-
+1(x>0)
根据题意,有f′(1)=-2,所以2a2-a-3=0,解得a=-1或a=
;
(2)f′(x)=
(x>0)
(1)当a>0时,因为x>0,
由f′(x)>0得(x-a)(x+2a)>0,解得x>a;
由f′(x)<0得(x-a)(x+2a)<0,解得0<x<a.
所以函数f(x)在(a,+∞)上单调递增,在(0,a)上单调递减;
(2)当a<0时,因为x>0,
由f′(x)>0得(x-a)(x+2a)>0,解得x>-2a;
由f′(x)<0得(x-a)(x+2a)<0,解得0<x<-2a.
所以函数f(x)在(-2a,+∞)上单调递增,在(0,-2a)上单调递减.
| a |
| x |
| 2a |
| x2 |
根据题意,有f′(1)=-2,所以2a2-a-3=0,解得a=-1或a=
| 3 |
| 2 |
(2)f′(x)=
| (x-a)(x+2a) |
| x2 |
(1)当a>0时,因为x>0,
由f′(x)>0得(x-a)(x+2a)>0,解得x>a;
由f′(x)<0得(x-a)(x+2a)<0,解得0<x<a.
所以函数f(x)在(a,+∞)上单调递增,在(0,a)上单调递减;
(2)当a<0时,因为x>0,
由f′(x)>0得(x-a)(x+2a)>0,解得x>-2a;
由f′(x)<0得(x-a)(x+2a)<0,解得0<x<-2a.
所以函数f(x)在(-2a,+∞)上单调递增,在(0,-2a)上单调递减.
点评:本题考查导数的几何意义,考查函数的单调区间,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
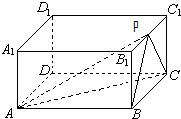 在正四棱柱ABCD-A1B1C1D1中,AB=2BB1=2,P为B1C1的中点.
在正四棱柱ABCD-A1B1C1D1中,AB=2BB1=2,P为B1C1的中点.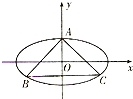 已知椭圆C中心是坐标原点O,焦点在x轴上,离心率e=
已知椭圆C中心是坐标原点O,焦点在x轴上,离心率e= 如图,长方体ABCD-A1B1C1D1中,AA1=AD=1,AB=2,点E是C1D1的中点.
如图,长方体ABCD-A1B1C1D1中,AA1=AD=1,AB=2,点E是C1D1的中点.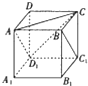 如图,正方体ABCD-A1B1C1D1,则下列五个命题:
如图,正方体ABCD-A1B1C1D1,则下列五个命题: