题目内容
某汽车制造厂有一条价值为60万元的汽车生产线，现要通过技术改造来提高其生产能力，进而提高产品的增加值．已知投入x万元用于技术改造，所获得的产品的增加值为（60-x）x2万元，并且技改投入比率
∈（0，5]．
（1）求技改投入x的取值范围；
（2）当技改投入多少万元时，所获得的产品的增加值为最大，其最大值为多少万元？
| x |
| 60-x |
（1）求技改投入x的取值范围；
（2）当技改投入多少万元时，所获得的产品的增加值为最大，其最大值为多少万元？
考点：分段函数的应用,函数模型的选择与应用
专题：应用题,导数的概念及应用
分析：（1）利用
∈（0，5]，x＞0，即可确定技改投入x的取值范围；
（2）求导函数，确定函数的单调性，即可求出产品增加值的最大值及相应x的值．
| x |
| 60-x |
（2）求导函数，确定函数的单调性，即可求出产品增加值的最大值及相应x的值．
解答：
解：（1）由题意，
∈（0，5]，x＞0，
∴0＜x≤50，
∴技改投入x的取值范围是（0，50]；
（2）设f（x）=（60-x）x2，x∈（0，50]，则f′（x）=-3x（x-40），
0＜x＜40时，f′（x）＞0；40＜x≤50时，f′（x）＜0，
∴x=40时，函数取得极大值，也是最大值3200万元．
| x |
| 60-x |
∴0＜x≤50，
∴技改投入x的取值范围是（0，50]；
（2）设f（x）=（60-x）x2，x∈（0，50]，则f′（x）=-3x（x-40），
0＜x＜40时，f′（x）＞0；40＜x≤50时，f′（x）＜0，
∴x=40时，函数取得极大值，也是最大值3200万元．
点评：本题的考点是根据实际问题选择函数类型，主要考查函数模型的构建，考查学生利用数学知识解决实际问题的能力，属于中档题．
练习册系列答案
相关题目
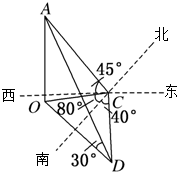某人在C点测得某塔在南偏西80°的O处，塔顶A的仰角为45°，此人沿南偏东40°方向前进10米到D处，测得塔顶A的仰角为30°，求塔OA的高度？
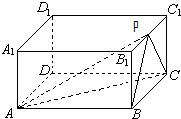在正四棱柱ABCD-A1B1C1D1中，AB=2BB1=2，P为B1C1的中点．
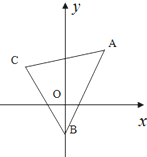如图，已知三角形的顶点为A（2，4），B（0，-2），C（-2，3）．求：
如图，长方体ABCD-A1B1C1D1中，AA1=AD=1，AB=2，点E是C1D1的中点．