题目内容
经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量y（千辆/小时）与汽车的平均速度υ（千米/小时）之间的函数关系为：y=
（υ＞0）．
（1）在该时段内，当汽车的平均速度υ为多少时，车流量最大？最大车流量为多少？（保留分数形式）
（2）若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？
| 920υ |
| υ2+3υ+1600 |
（1）在该时段内，当汽车的平均速度υ为多少时，车流量最大？最大车流量为多少？（保留分数形式）
（2）若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？
考点：基本不等式在最值问题中的应用
专题：应用题,不等式的解法及应用
分析：（1）根据基本不等式性质可知y=
=
≤
，进而求得y的最大值．根据等号成立的条件求得此时的平均速度．
（2）在该时间段内车流量超过10千辆/小时时，解不等式即可求出v的范围．
| 920υ |
| υ2+3υ+1600 |
| 920 | ||
3+(v+
|
| 920 |
| 83 |
（2）在该时间段内车流量超过10千辆/小时时，解不等式即可求出v的范围．
解答：
解：（1）依题意，y=
=
≤
，
当且仅当v=
，即v=40时，上式等号成立，
∴ymax=
（千辆/时）．
∴如果要求在该时段内车流量超过10千辆/时，则汽车的平均速度应大于25km/h且小于64km/h．当v=40km/h时，车流量最大，最大车流量约为
千辆/时；
（2）由条件得
＞10，
整理得v2-89v+1600＜0，
即（v-25）（v-64）＜0．解得25＜v＜64．
| 920υ |
| υ2+3υ+1600 |
| 920 | ||
3+(v+
|
| 920 |
| 83 |
当且仅当v=
| 1600 |
| v |
∴ymax=
| 920 |
| 83 |
∴如果要求在该时段内车流量超过10千辆/时，则汽车的平均速度应大于25km/h且小于64km/h．当v=40km/h时，车流量最大，最大车流量约为
| 920 |
| 83 |
（2）由条件得
| 920υ |
| υ2+3υ+1600 |
整理得v2-89v+1600＜0，
即（v-25）（v-64）＜0．解得25＜v＜64．
点评：本题主要考查了基本不等式在最值问题中的应用．要特别留意等号取得的条件．
练习册系列答案
相关题目
已知数列an=3n-4，则29是该数列的（ ）
| A、第11项 | B、第13项 |
| C、第14项 | D、第15项 |
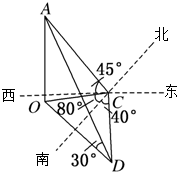某人在C点测得某塔在南偏西80°的O处，塔顶A的仰角为45°，此人沿南偏东40°方向前进10米到D处，测得塔顶A的仰角为30°，求塔OA的高度？
某高三7班30名男生1000米跑统测成绩的茎叶图（如果某学生1000米测试成绩是x分y秒，x为茎，y为叶）如图．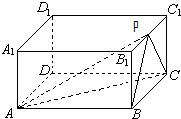
在正四棱柱ABCD-A1B1C1D1中，AB=2BB1=2，P为B1C1的中点．