题目内容
已知函数m(x)=log4(4x+1),n(x)=kx(k∈R)
(1)当x>0时,F(x)=m(x),且F(x)为R上的奇函数,求x<0时F(x)的表达式;
(2)若f(x)=m(x)+n(x)为偶函数,求k的值;
(3)对(2)中的函数f(x),设g(x)=log4(2x-
a),若函数f(x)与g(x)的图象有公共点,求实数a的取值范围.
(1)当x>0时,F(x)=m(x),且F(x)为R上的奇函数,求x<0时F(x)的表达式;
(2)若f(x)=m(x)+n(x)为偶函数,求k的值;
(3)对(2)中的函数f(x),设g(x)=log4(2x-
| 4 |
| 3 |
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:(1)令x<0,则-x>0,运用已知区间上的解析式,结合奇函数的定义,即可得到所求;
(2)运用偶函数的定义,结合对数的运算性质,化简整理,即可求得k;
(3)函数的图象有公共点,即为方程f(x)=g(x)有解,化简方程,再由指数函数的值域,即可求得a的范围.
(2)运用偶函数的定义,结合对数的运算性质,化简整理,即可求得k;
(3)函数的图象有公共点,即为方程f(x)=g(x)有解,化简方程,再由指数函数的值域,即可求得a的范围.
解答:
解:(1)令x<0,则-x>0,
由于当x>0时,F(x)=log4(4x+1),
则F(-x)=log4(4-x+1),
又F(x)为R上的奇函数,则F(-x)=-F(x),
则有x<0时,F(x)=-log4(4-x+1);
(2)f(x)=m(x)+n(x)=log4(4x+1)+kx,
由于f(x)为偶函数,则f(-x)=f(x),
即log4(4-x+1)-kx=log4(4x+1)+kx,
即有2kx=log4
=log4
=-x,
即有k=-
;
(3)f(x)=log4(4x+1)-
x,令f(x)=g(x),
则log4
=log4(2x-
a),
即有
=2x-
a,即为2-x=-
a,
由于2-x>0,则a<0,
则函数f(x)与g(x)的图象有公共点,
即有a的取值范围是(-∞,0).
由于当x>0时,F(x)=log4(4x+1),
则F(-x)=log4(4-x+1),
又F(x)为R上的奇函数,则F(-x)=-F(x),
则有x<0时,F(x)=-log4(4-x+1);
(2)f(x)=m(x)+n(x)=log4(4x+1)+kx,
由于f(x)为偶函数,则f(-x)=f(x),
即log4(4-x+1)-kx=log4(4x+1)+kx,
即有2kx=log4
| 4-x+1 |
| 4x+1 |
| 1 |
| 4x |
即有k=-
| 1 |
| 2 |
(3)f(x)=log4(4x+1)-
| 1 |
| 2 |
则log4
| 4x+1 |
| 2x |
| 4 |
| 3 |
即有
| 4x+1 |
| 2x |
| 4 |
| 3 |
| 4 |
| 3 |
由于2-x>0,则a<0,
则函数f(x)与g(x)的图象有公共点,
即有a的取值范围是(-∞,0).
点评:本题考查函数的奇偶性的判断和运用:求解析式,求参数,考查对数的运算性质和指数函数的值域,属于基础题.

练习册系列答案
相关题目
 如图所示,椭圆
如图所示,椭圆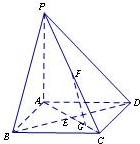 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.