题目内容
6．设集合A={x|x（5-x）＞4}，B={x|x≤a}，若A∪B=B，则a的值可以是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 由已知得A⊆B，由此能求出实数a的取值范围，可得结论．
解答 解：集合A={x|x（5-x）＞4}={x|1＜x＜4}，
∵A∪B=B，
∴A⊆B，
∵B={x|x≤a}，∴a≥4．
∴a的值可以是4，
故选D．
点评 本题考查实数的取值范围的求法，是基础题，解题时要注意并集的性质的合理运用．
练习册系列答案
应用题作业本系列答案
相关题目
16．某商家在网上销售一种商品，从该商家的销售数据中抽取6天的价格与销量的对应数据，如下表所示：
（Ⅰ）由表中数据，看出可用线性回归模型拟合y与x的关系，试求y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并预测当价格为1000元时，每天的商品的销量为多少；
（Ⅱ）若以从这6天中随机抽取2天，至少有1天的价格高于700元的概率．
参考数据：$\sum_{i=1}^{6}$xiyi=3050，$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271．
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$．
| 价格x（百元） | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y（件/天） | 90 | 84 | 83 | 80 | 75 | 68 |
（Ⅱ）若以从这6天中随机抽取2天，至少有1天的价格高于700元的概率．
参考数据：$\sum_{i=1}^{6}$xiyi=3050，$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271．
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$．
17．某市对大学生毕业后自主创业人员给予小额贷款补贴，贷款期限分为6个月、12个月、18个月、24个月、36个月五种，对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元，从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计，选取贷款期限的频数如表：
（Ⅰ）若小王准备申请此项贷款，求其获得政府补贴不超过300元的概率（以上表中各项贷款期限的频率作为2017年自主创业人员选择各种贷款期限的概率）；
（Ⅱ）若小王和小李同时申请此项贷款，求两人所获得政府补贴之和不超过600元的概率．
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
（Ⅱ）若小王和小李同时申请此项贷款，求两人所获得政府补贴之和不超过600元的概率．
14．
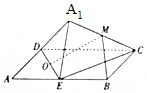如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE（A1∉平面ABCD），若M、O分别为线段A1C、DE的中点，则在△ADE翻转过程中，下列说法错误的是（ ）
如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE（A1∉平面ABCD），若M、O分别为线段A1C、DE的中点，则在△ADE翻转过程中，下列说法错误的是（ ）| A． | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B． | 异面直线BM与A1E所成角是定值 | |
| C． | 一定存在某个位置，使DE⊥MO | |
| D． | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
1．已知集合A={y|0≤y＜2，y∈N}，B={x|x2-4x-5≤0，x∈N}，则A∩B=（ ）
| A． | {1} | B． | {0，1} | C． | [0，2） | D． | ∅ |
18．
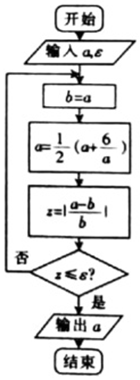十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法，相较于二分法更具优势，如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图，若输入a=2，?=0.02，则输出的结果为（ ）
十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法，相较于二分法更具优势，如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图，若输入a=2，?=0.02，则输出的结果为（ ）| A． | 3 | B． | 2.5 | C． | 2.45 | D． | 2.4495 |
16．
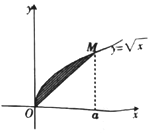如图，点M在曲线y=$\sqrt{x}$，若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$，则实数a等于（ ）
如图，点M在曲线y=$\sqrt{x}$，若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$，则实数a等于（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | 1 | D． | 2 |