题目内容
△ABC中,已知tanC=
.
(1)sin2
的值;
(2)若AB=2
,AC=6,D为AC的中点,求BD的长.
| ||
| 2 |
(1)sin2
| A+B |
| 2 |
(2)若AB=2
| 5 |
考点:余弦定理
专题:解三角形
分析:(1)由同角三角函数基本关系可得
结合cosC>0,解方程组可得cosC,由二倍角公式可得sin2
=
=
,代入计算可得;(2)由余弦定理可得AB2=AC2+BC2-2AC•BCcosC,代入数值可解得BC,在△BCD中由余弦定理可得所求.
|
| A+B |
| 2 |
| 1-cos(A+B) |
| 2 |
| 1+cosC |
| 2 |
解答:
解:(1)∵tanC=
,且0<C<π,∴cosC>0
由同角三角函数基本关系可得
,
解方程组可得cosC=
,
∴sin2
=
=
=
(2)由余弦定理可得AB2=AC2+BC2-2AC•BCcosC,
代入数值可得(2
)2=62+BC2-2×6×
BC,解得BC=4,
在△BCD中由余弦定理可得BD2=CD2+BC2-2CD•BCcosC
=32+42-2×3×4×
=9,∴BD=3
| ||
| 2 |
由同角三角函数基本关系可得
|
解方程组可得cosC=
| 2 |
| 3 |
∴sin2
| A+B |
| 2 |
| 1-cos(A+B) |
| 2 |
| 1+cosC |
| 2 |
| 5 |
| 6 |
(2)由余弦定理可得AB2=AC2+BC2-2AC•BCcosC,
代入数值可得(2
| 5 |
| 2 |
| 3 |
在△BCD中由余弦定理可得BD2=CD2+BC2-2CD•BCcosC
=32+42-2×3×4×
| 2 |
| 3 |
点评:本题考查解三角形,涉及余弦定理和同角三角函数的基本关系,属中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
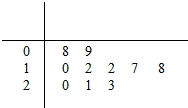 现从某100件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,
现从某100件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,