题目内容
已知函数f（x）=2
sin（
+
）•cos（
+
）-sin（π+x）．
（1）求f（x）的最小正周期．
（2）若将f（x）的图象向右平移
个单位，得到函数g（x）的图象，求函数g（x）在区间[0，π]上的值域．
| 3 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
（1）求f（x）的最小正周期．
（2）若将f（x）的图象向右平移
| π |
| 6 |
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法,函数y=Asin（ωx+φ）的图象变换
专题：计算题,三角函数的图像与性质
分析：（1）先利用辅助角公式化简函数，再求f（x）的最小正周期．
（2）确定g(x)=2sin(x+
)，再求函数g（x）在区间[0，π]上的值域．
（2）确定g(x)=2sin(x+
| π |
| 6 |
解答：
解：由题设可得f(x)=
cosx+sinx=2sin(x+
)
（1）函数最小正周期为2π；
（2）将f（x）的图象向右平移
个单位，得到g(x)=2sin(x+
)．
∵0≤x≤π，
∴
≤x+
≤
π，
∴g（x）值域为[-1，2]．
| 3 |
| π |
| 3 |
（1）函数最小正周期为2π；
（2）将f（x）的图象向右平移
| π |
| 6 |
| π |
| 6 |
∵0≤x≤π，
∴
| π |
| 6 |
| π |
| 6 |
| 7 |
| 6 |
∴g（x）值域为[-1，2]．
点评：本题考查三角函数的恒等变换、三角函数的周期及其求法、三角函数的图象变换等知识，熟练掌握有关基础知识解决该类题目的关键．
练习册系列答案
相关题目
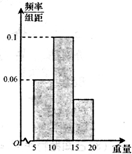如图是一容量为100的样本的重量的频率分布直方图，样本重量均在[5，20]内，其分组为[5，10），[10，15），[15，20]，则样本重量落在[15，20]内的频数为