题目内容
已知圆C的半径为2，圆心在x轴的正半轴上，直线3x-4y+4=0与圆C相切，
（1）求圆C的方程；
（2）过点Q（0，-3）斜率为k的直线l与圆C交于不同的两点A（x1，y1），B（x2，y2），
①当k=3时，求x1•x2+y1•y2的值；
②当x1•x2+y1•y2=8时，求直线l的方程．
（1）求圆C的方程；
（2）过点Q（0，-3）斜率为k的直线l与圆C交于不同的两点A（x1，y1），B（x2，y2），
①当k=3时，求x1•x2+y1•y2的值；
②当x1•x2+y1•y2=8时，求直线l的方程．
考点：直线和圆的方程的应用
专题：综合题,直线与圆
分析：（1）设出圆心坐标为（a，0）且a＞0，利用圆与直线3x-4y+4=0相切得到圆心到直线的距离等于半径2求出a，即可得到圆的标准方程；
（2）①当k=3时，直线l的方程y+3=3x，代入圆的方程，利用韦达定理，即可求x1•x2+y1•y2的值；
②利用韦达定理，结合x1•x2+y1•y2=8，即可求直线l的方程．
（2）①当k=3时，直线l的方程y+3=3x，代入圆的方程，利用韦达定理，即可求x1•x2+y1•y2的值；
②利用韦达定理，结合x1•x2+y1•y2=8，即可求直线l的方程．
解答：
解：（1）设圆心坐标为（a，0）且a＞0，
∵圆与直线3x-4y+4=0相切，
∴圆心到直线的距离等于半径2，即
=2，求得a=2或a=-
（舍去），
∴a=2
∴圆心坐标为（2，0），半径为2的圆的标准方程为：（x-2）2+y2=4；
（2）①当k=3时，直线l的方程y+3=3x，
代入圆的方程，可得10x2-22x+9=0，
∴x1•x2=
，x1+x2=
，
∴x1•x2+y1•y2=x1•x2+（3x1-3）（3x2-3）=10x1•x2-9（x1+x2）+9=-
②设直线l的方程为y+3=kx，
代入圆的方程，可得（1+k2）x2-（4+6k）x+9=0，
∴x1•x2=
，x1+x2=
，
∴x1•x2+y1•y2=x1•x2+（kx1-3）（kx2-3）=（1+k2）x1•x2-3k（x1+x2）+9
=9-3k•
+9，
∵x1•x2+y1•y2=8，
∴9-3k•
+9=8，
∴k=
，
经检验k=
，满足题意，
∴直线l的方程为y=
x-3．
∵圆与直线3x-4y+4=0相切，
∴圆心到直线的距离等于半径2，即
| |3a+4| | ||
|
| 14 |
| 3 |
∴a=2
∴圆心坐标为（2，0），半径为2的圆的标准方程为：（x-2）2+y2=4；
（2）①当k=3时，直线l的方程y+3=3x，
代入圆的方程，可得10x2-22x+9=0，
∴x1•x2=
| 9 |
| 10 |
| 11 |
| 5 |
∴x1•x2+y1•y2=x1•x2+（3x1-3）（3x2-3）=10x1•x2-9（x1+x2）+9=-
| 9 |
| 5 |
②设直线l的方程为y+3=kx，
代入圆的方程，可得（1+k2）x2-（4+6k）x+9=0，
∴x1•x2=
| 9 |
| 1+k2 |
| 4+6k |
| 1+k2 |
∴x1•x2+y1•y2=x1•x2+（kx1-3）（kx2-3）=（1+k2）x1•x2-3k（x1+x2）+9
=9-3k•
| 4+6k |
| 1+k2 |
∵x1•x2+y1•y2=8，
∴9-3k•
| 4+6k |
| 1+k2 |
∴k=
-3±
| ||
| 4 |
经检验k=
-3+
| ||
| 4 |
∴直线l的方程为y=
-3+
| ||
| 4 |
点评：本题考查学生理解圆与直线相切时得到圆心到直线的距离等于半径，会用点到直线的距离公式求点到直线的距离，会根据圆心坐标和半径写出圆的标准方程，考查直线与圆的位置关系，考查韦达定理的运用，属于中档题．
练习册系列答案
相关题目
已知定义在R上的函数f（x）=ex+x2-x+sinx，则曲线y=f（x）在点（0，f（0））处的切线方程是（ ）
| A、y=2x-1 |
| B、y=x+1 |
| C、y=3x-2 |
| D、y=-2x+3 |
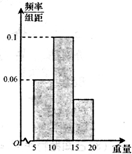如图是一容量为100的样本的重量的频率分布直方图，样本重量均在[5，20]内，其分组为[5，10），[10，15），[15，20]，则样本重量落在[15，20]内的频数为