Question

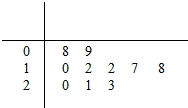现从某100件中药材中随机抽取10件，以这10件中药材的重量（单位：克）作为样本，样本数据的茎叶图如图，
（Ⅰ）求样本数据的中位数、平均数，并估计这100件中药材的总重量；
（Ⅱ）记重量在15克以上的中药材为优等品，在该样本的优等品中，随机抽取2件，求这2件中药材的重量之差不超过2克的概率．

Answer 1

考点：古典概型及其概率计算公式,茎叶图

专题：概率与统计

分析：（Ⅰ）根据茎叶图数据直接求样本数据的中位数、平均数即可；！
（Ⅱ）列举从10件中药材的优等品中随机抽取2件的所有基本事件，找出2件优等品的重量之差不超过2克所包含的事件，利用古典概型概率公式计算即可．

解答： 解：（Ⅰ）样本数据的中位数是

12+17

2

=14.5，
样本数据的平均数是

8+9+10+12+12+17+18+20+21+23

10

=15；
根据样本数据估计总体的思想可得，这100件中药材重量的平均数是15克，
因此，估计这100件中药材的总重量约为100×15=1500克．
（Ⅱ）这10件中药材的优等品的重量有17克、18克、20克、21克、23克．
从10件中药材的优等品中随机抽取2件，所有基本事件有：
（17，18），（17，20），（17，21），（17，23），（18，20），（18，21），
（18，23），（20，21），（20，23），（21，23）共10个．
记“2件优等品的重量之差不超过2克”为事件A，
则事件A的基本事件有：（17，18），（18，20），），（20，21），（21，23）共4个．
∴P（A）=

4

10

=

2

5

．
∴这2件中药材的重量之差不超过2克的概率为

2

5

．

点评：本题考查茎叶图、平均数、中位数、古典概型等知识，以及数据处理能力，样本估计总体的数学思想．属于中档题．