题目内容
(1)若函数y=mx2-6x+2的图象与x轴只有一个公共点,求m的值;
(2)若方程4(x2-3x)+k-3=0没有实数根,求k的取值范围.
(2)若方程4(x2-3x)+k-3=0没有实数根,求k的取值范围.
考点:函数的零点,二次函数的性质
专题:计算题,函数的性质及应用
分析:(1)讨论函数是否是二次函数,从而求m的值;
(2)原方程可化为4x2-12x+k-3=0,从而可得△=144-4•4•(k-3)=192-16k<0,从而解得.
(2)原方程可化为4x2-12x+k-3=0,从而可得△=144-4•4•(k-3)=192-16k<0,从而解得.
解答:
解:(1)若m=0时y=-6x+2符合题意,
若m≠0,则△=36-8m=0,得m=
;
所以m=0或m=
时,y=mx2-6x+2的图象与x轴只有一个公共点.
(2)原方程可化为4x2-12x+k-3=0,
当方程判别式满足△<0时原方程无实数根,
又△=144-4•4•(k-3)=192-16k,
解得k>12,
所以当k>12时,原方程无实数根.
若m≠0,则△=36-8m=0,得m=
| 9 |
| 2 |
所以m=0或m=
| 9 |
| 2 |
(2)原方程可化为4x2-12x+k-3=0,
当方程判别式满足△<0时原方程无实数根,
又△=144-4•4•(k-3)=192-16k,
解得k>12,
所以当k>12时,原方程无实数根.
点评:本题考查了二次函数的性质应用及函数的零点与方程的根的关系应用,属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
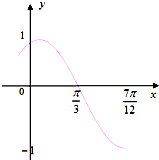 函数f(x)=sin(ωx+φ)的图象如图所示,其中ω>0,|φ|<
函数f(x)=sin(ωx+φ)的图象如图所示,其中ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
