题目内容

已知△ABC的面积为
3
，且
AB
•
AC
=2．
（1）求角A的大小；
（2）求
2si
n
2
 
A
2
+2sin
A
2
cos
A
2
-1
cos(
π
4
-A)
的值．
考点：三角函数的恒等变换及化简求值,平面向量数量积的运算
专题：计算题
分析：（1）根据
AB
•
AC
=2，△ABC的面积为
3
，利用向量的数量积公式及三角形的面积公式，即可求得A的值；
（2）利用二倍角公式化简函数，即可求得结论．
解答： 解：（1）∵
AB
•
AC
=2
∴bccosA=2
∵△ABC的面积为
3
，
∴
1
2
bcsinA=
3

∴tanA=
3

∵0＜A＜π
∴A=
π
3
；
（2）
2si
n
2
 
A
2
+2sin
A
2
cos
A
2
-1
cos(
π
4
-A)
=
-cosA+sinA
cos(
π
4
-
π
3
)
=
3
2
-
1
2
2
2
×
1
2
+
2
2
×
3
2
=
2(
3
-1)
2
+
3
=2
2
-
6
点评：本题考查向量的数量积公式，考查三角形的面积公式，考查三角函数的化简，属于中档题．
练习册系列答案
相关题目
函数f（x）=x2+ax+3，x∈[0，2]
（Ⅰ）若a=2，求f（x）的最值，并说明当f（x）取最值时的x的值；
（Ⅱ）若f（x）≥0恒成立，求a的取值范围．
已知平面向量
a
与
b
不共线，若存在非零实数x，y，使得
c
=
a
+2x
b
，
d
=-y
a
+2（2-x2）
b
．
（1）当
c
=
d
时，求x，y的值；
（2）若
a
=（cos
π
6
，sin(-
π
6
)），
b
=（sin
π
6
，cos
π
6
），且
c
⊥
d
，试求函数y=f（x）的表达式．
一颗正方体骰子，共六个面的点数分别是1、2、3、4、5、6，将这颗骰子连续掷三次观察向上的点数，则三次点数和为16的概率是（　　）
A、
1
6
B、
1
18
C、
1
36
D、
1
72
设An为（1+x）n+1的展开式中含xn-1项的系数，Bn为 （1+x）n-1的展开式中二项式系数的和，n∈N*，则能使An≥Bn成立的n的最大值是
 
．
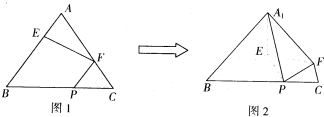如图1，在正三角形ABC中，已知AB=5，E、F、P分别是AB、AC、BC边上的点，设AE=2x，CF=CP=x，0＜x＜
5
2
，将△ABC沿EF折起到△A1EF的位置，使二面角A1-EF-B的大小为
π
2
，连接A1B、A1P（如图2）．
（1）求证：PF∥平面A1EB；
（2）若EF⊥平面A1EB，求x的值；
（3）当EF⊥平面A1EB时，求平面A1BP与平面A1EF所成锐二面角的余弦值．
△ABC的三个内角分别为A、B、C，则下列条件中能够确定△ABC为钝角三角形的条件共有
 
个．
①A：B：C=7：20：25；
②sinA：sinB：sinC=7：20：25；
③cosA：cosB：cosC=7：20：25；
④tanA：tanB：tanC=7：20：25．
若不等式a＞2sinxcosx+
3
cos2x恒成立，则实数a的取值范围为
 
．
{ an}是非常数等差数列，an为通项，Sn为前项的和，则
lim
n→∞
Sn
nan
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网