题目内容

若不等式a＞2sinxcosx+
3
cos2x恒成立，则实数a的取值范围为
 
．
考点：三角函数的化简求值,函数恒成立问题
专题：计算题
分析：令f（x）=2sinxcosx+
3
cos2x，则f（x）=2sin（2x+
π
3
），由题意可得，于是问题得到解决．
解答： 解：令f（x）=2sinxcosx+
3
cos2x=2sin（2x+
π
3
），
∴不等式a＞2sinxcosx+
3
cos2x恒成立，
就是a＞f（x）max成立，而f（x）max=2，
∴a＞2．
∴实数a的取值范围为（2，+∞）．
点评：本题考查三角函数的化简求值，理解题意得到a＞f（x）max是关键，属于基础题．
练习册系列答案
相关题目
在平面直角坐标系中，若不等式组
x+y-1≥0
x-1≤0
ax-y+1≥0
（α为常数）所表示的平面区域内的面积等于2，则a的值为多少？
已知△ABC的面积为
3
，且
AB
•
AC
=2．
（1）求角A的大小；
（2）求
2si
n
2
 
A
2
+2sin
A
2
cos
A
2
-1
cos(
π
4
-A)
的值．
对定义在[0，1]上，并且同时满足以下两个条件的函数f（x）称为G函数．
①对任意的x∈[0，1]，总有f（x）≥0；
②当x1≥0，x2≥0，x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立．
已知函数g（x）=x2与h（x）=a•2x-1是定义在[0，1]上的函数．
（1）试问函数g（x）是否为G函数？并说明理由；
（2）若函数h（x）是G函数，求实数a的值；
（3）在（2）的条件下，若方程g（2x-1）+h（x）=m有解，求实m的取值范围．
设两个方程x2-4x+lga=0，x2-4x+lgb=0（a≠b）的四个根组成一个公差为2的等差数列，则ab的值为
 
．
已知等差数列{an}的前n项和为Sn，首项为1的等比数列{bn}的公比为q，S2=a3=b3，且a1，a3，b2成等比数列．
（1）求{an}和{bn}的通项公式；
（2）设数列{bn}的前n项和为Tn，若2Sn-nan=b+loga（2Tn+1）对一切正整数n成立，求实数a，b的值．
现有大小形状完全相同的标号为i的i个球（i=1，2，3），现从中随机取出2个球，记取出的这两个球的标号数之和为ξ，则随机变量的数学期望Eξ=
 
．
若集合M={x|x2+x-6=0}，N={x|ax-1=0}，且M∩N=N，则实数a的取值组成的集合是 （　　）
A、{
1
2
，-
1
3
}
B、{-
1
2
，
1
3
}
C、{-
1
2
，0，
1
3
}
D、{-
1
3
，0，
1
2
}
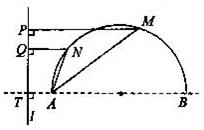如图，已知半圆的直径|AB|=20，l为半圆外一直线，且与BA的延长线交于点T，|AT|=4，半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件
|MP|
|MA|
=
|NQ|
|NA|
=1，则|AM|+|AN|的值为（　　）
A、22B、20C、18D、16

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网