题目内容
设a是实数，则“a=1”是“a2=1”的（ ）
| A、充分而不必要条件 |
| B、必要而不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：若a=1，则a2=1成立，即充分性成立．
当a=-1，满足a2=1，但a=1不成立，即必要性不成立，
故“a=1”是“a2=1”的充分不必要条件，
故选：A．
当a=-1，满足a2=1，但a=1不成立，即必要性不成立，
故“a=1”是“a2=1”的充分不必要条件，
故选：A．
点评：本题主要考查充分条件和必要条件的判断，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
四面体P-ABC中，若PA=PB=PC，则点P在平面ABC内的射影点O是三角形ABC的（ ）
| A、内心 | B、外心 | C、垂心 | D、重心 |
已知平面α，β所成的二面角为80°，P为α，β外一定点，则过点P作直线与α，β都成30°的直线有（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
若A、B、C三点共线，O是这条直线外一点，且满足m
-2
+
=
，若
=λ
，则λ的值为（ ）
| OA |
| OB |
| OC |
| 0 |
| BA |
| AC |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（ ）
A、f（x）=
| ||
| B、f（x）=x2-1 | ||
| C、f（x）=x3 | ||
| D、f（x）=2-x |
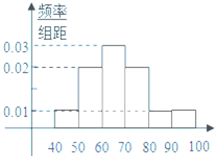某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生成绩进行统计，得到如图所示的样本频率分布直方图．若规定60分及以上为合格，则估计这1000名学生中合格人数是（ ）名．| A、400 | B、600 |
| C、700 | D、800 |
过点（-1，3）且平行于直线x-2y+3=0的直线方程为（ ）
| A、x-2y=0 |
| B、2x+y-1=0 |
| C、x-2y+7=0 |
| D、2x+y-5=0 |