题目内容
已知函数f（x）=（1-2x3）6，则f′（1）等于（ ）
| A、0 | B、-6 | C、-36 | D、36 |
考点：导数的运算
专题：导数的概念及应用
分析：根据复合函数求导的法则进行求导，然后再代入x=1，问题得以解决．
解答：
解：∵f（x）=（1-2x3）6，
∴f′（x）=6（1-2x3）5（1-2x3）′=6（1-2x3）5（-6x2），
∴f′（1）=6（1-2×13）5（-6×12）=36．
故选：D
∴f′（x）=6（1-2x3）5（1-2x3）′=6（1-2x3）5（-6x2），
∴f′（1）=6（1-2×13）5（-6×12）=36．
故选：D
点评：本题主要考查了复合函数的求导问题，掌握求导法则是关键，属于基础题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
已知平面α，β所成的二面角为80°，P为α，β外一定点，则过点P作直线与α，β都成30°的直线有（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（ ）
A、f（x）=
| ||
| B、f（x）=x2-1 | ||
| C、f（x）=x3 | ||
| D、f（x）=2-x |
已知数列{an}满足a1=2，an+1=
（n∈N*），则a30=（ ）
| an-1 |
| an+1 |
| A、2 | ||
B、
| ||
C、-
| ||
| D、-3 |
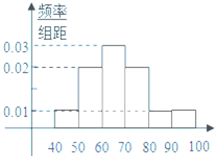某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生成绩进行统计，得到如图所示的样本频率分布直方图．若规定60分及以上为合格，则估计这1000名学生中合格人数是（ ）名．| A、400 | B、600 |
| C、700 | D、800 |
复数1-2i（i是虚数单位）的虚部是（ ）
| A、2i | B、-2i | C、2 | D、-2 |
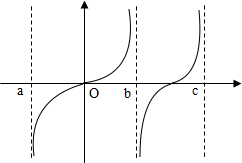已知函数f（x），x∈（a，b）∪（b，c）的图象如图所示，有三个同学对此函数的单调性作出如下的判断：