题目内容
关于x的不等式x2-ax-6a2<0(a>0)的解集为(x1,x2),且x2-x1=10,则a=( )
| A、2 | ||
| B、5 | ||
C、
| ||
D、
|
考点:一元二次不等式的应用
专题:函数的性质及应用,不等式的解法及应用
分析:利用不等式的解集以及韦达定理得到两根关系式,然后与已知条件化简求解a的值即可.
解答:
解:因为关于x的不等式x2-ax-6a2<0(a>0)的解集为(x1,x2),
所以x1+x2=a…①,x1•x2=-6a2…②,又x2-x1=10…③,
①2-4×②可得(x2-x1)2=25a2,代入③可得,102=25a2,解得a=±2,
因为a>0,所以a=2.
故选:A.
所以x1+x2=a…①,x1•x2=-6a2…②,又x2-x1=10…③,
①2-4×②可得(x2-x1)2=25a2,代入③可得,102=25a2,解得a=±2,
因为a>0,所以a=2.
故选:A.
点评:本题考查二次不等式的解法,韦达定理的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
A、f(x)=
| ||
| B、f(x)=x2-1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |
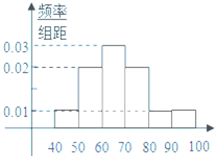 某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是( )名.
某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是( )名.| A、400 | B、600 |
| C、700 | D、800 |
复数1-2i(i是虚数单位)的虚部是( )
| A、2i | B、-2i | C、2 | D、-2 |
空间有四个点,其中任意三点,都不在同一条直线上,那么它们可确定( )
| A、三个或两个平面 |
| B、四个或三个平面 |
| C、三个或一个平面 |
| D、四个或一个平面 |
过点(-1,3)且平行于直线x-2y+3=0的直线方程为( )
| A、x-2y=0 |
| B、2x+y-1=0 |
| C、x-2y+7=0 |
| D、2x+y-5=0 |