题目内容
10.给出如下四个命题:①e${\;}^{\frac{2}{e}}$>2②ln2>$\frac{2}{3}$③π2<3π④$\frac{ln2}{2}$<$\frac{lnπ}{π}$,正确的命题的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①利用分析法和构造函数,利用导数和函数的最值得关系即可判断,②根据对数的运算性质即可判断,③利用中间量即可判断,④两边取对数即可判断.
解答 解:①要证e${\;}^{\frac{2}{e}}$>2,只要证$\frac{2}{e}$>ln2,即2>eln2,
设f(x)=elnx-x,x>0,
∴f′(x)=$\frac{e}{x}$-1=$\frac{e-x}{x}$,
当0<x<e时,f′(x)>0,函数单调递增,
当x>e时,f′(x)<0,函数单调递减,
∴f(x)<f(e)=elne-e=0,
∴f(2)=eln2-2<0,
即2>eln2,
∴e${\;}^{\frac{2}{e}}$>2,因此正确
②∵3ln2=ln8>ln2.82>lne2=2.∴ln2>$\frac{2}{3}$,因此正确,
③π2<42=16,3π>33=27,因此π2<3π,③正确,
④∵2π<π2,∴$\frac{ln2}{2}$<$\frac{lnπ}{π}$,④正确;
正确的命题的个数为4个,
故选:D.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AB=2,若该四棱锥的所有顶点都在体积为$\frac{9π}{2}$的同一球面上,则PA的长为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
18.若实数x,y满足约束条件$\left\{\begin{array}{l}x-1≥0\\ x-y≤0\\ x+y-6≤0\end{array}\right.$,则x-2y的最大值为( )
| A. | -9 | B. | -3 | C. | -1 | D. | 3 |
5.一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:
(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.
| x | [11,13) | [13,15) | [15,17) | [17,19) | [19,21) | [21,23) |
| 频数 | 2 | 12 | 34 | 38 | 10 | 4 |
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.
15.设函数f(x)=$\left\{\begin{array}{l}{a{x}^{2}+x,x≥0}\\{-a{x}^{2}+x,x<0}\end{array}\right.$当x∈[-$\frac{1}{2}$,$\frac{1}{2}$]时,恒有f(x+a)<f(x),则实数a的取值范围是( )
| A. | ($\frac{1-\sqrt{5}}{2}$,$\frac{1+\sqrt{5}}{2}$) | B. | (-1,$\frac{1+\sqrt{5}}{2}$) | C. | ($\frac{1-\sqrt{5}}{2}$,0) | D. | ($\frac{1-\sqrt{5}}{2}$,-$\frac{1}{2}$] |
2.定义域为R的函数f(x)的图象关于直线x=1对称,当a∈[0,l]时,f(x)=x,且对任意x∈R只都有f(x+2)=-f(x),g(x)=$\left\{\begin{array}{l}f(x)(x≥0)\\-{log_{2013}}(-x)(x<0)\end{array}\right.$,则方程g(x)-g(-x)=0实数根的个数为( )
| A. | 1006 | B. | 1007 | C. | 2012 | D. | 2014 |
19.(文)已知是虚数单位,则$\frac{3+i}{1-i}$=( )
| A. | 1+2i | B. | 2+i | C. | -1+i | D. | -1-i |
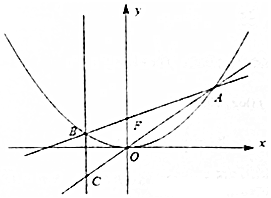 已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.
已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.