题目内容
已知F1,F2是双曲线x2-5y2=5的两焦点,点P在双曲线上,且△F1PF2的面积为
,则∠F1PF2的大小为 .
| 3 |
考点:双曲线的简单性质
专题:计算题,解三角形,圆锥曲线的定义、性质与方程
分析:利用双曲线的定义、三角形的面积、余弦定理建立方程,即可得出结论.
解答:
解:双曲线x2-5y2=5可化为:
-y2=1,
则a=
,b=1,c=
,
设∠F1PF2=α,|PF1|=m,|PF2|=n,m>n,则m-n=2
①,
∵△F1PF2的面积为
,
∴
mnsinα=
②,
又∵24=m2+n2-2mncosα③,
由①②③,由配方消去m,n,可得
=
,
即
=
,即有tan
=
,
可得α=
.
故答案为:
.
| x2 |
| 5 |
则a=
| 5 |
| 6 |
设∠F1PF2=α,|PF1|=m,|PF2|=n,m>n,则m-n=2
| 5 |
∵△F1PF2的面积为
| 3 |
∴
| 1 |
| 2 |
| 3 |
又∵24=m2+n2-2mncosα③,
由①②③,由配方消去m,n,可得
| 1-cosα |
| sinα |
| ||
| 3 |
即
2sin2
| ||||
2sin
|
| ||
| 3 |
| α |
| 2 |
| ||
| 3 |
可得α=
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题主要考查了双曲线的简单性质、三角形面积的计算.要灵活运用双曲线的定义及焦距、实轴、虚轴等之间的关系.

练习册系列答案
相关题目
设a,b∈R,则“a+b>4”是“a>2,且b>2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
设a,b是非零实数,若a<b,则下列不等式成立的是( )
| A、a2<b2 | ||||
B、
| ||||
| C、2a<2b | ||||
D、
|

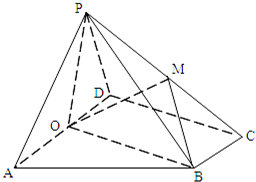 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC.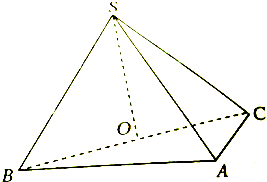 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.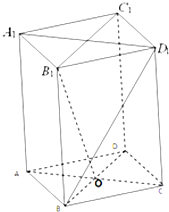 如图,四棱柱中A1B1C1D1-ABCD,底面ABCD为边长为2的菱形,侧棱长为3,且∠B1BA=∠B1BC=∠ABC=60°.
如图,四棱柱中A1B1C1D1-ABCD,底面ABCD为边长为2的菱形,侧棱长为3,且∠B1BA=∠B1BC=∠ABC=60°.