题目内容
已知向量
=(1,1,0),
=(-1,0,2),且k
+
与
互相垂直,则k的值是( )
| a |
| b |
| a |
| b |
| b |
| A、-5 | ||
B、
| ||
C、
| ||
| D、5 |
考点:向量的数量积判断向量的共线与垂直
专题:空间向量及应用
分析:利用向量垂直的性质求解.
解答:
解:∵向量
=(1,1,0),
=(-1,0,2),且k
+
与
互相垂直,
∴(k
+
)•
=(k-1,k,2)•(-1,0,2)=1-k+0+4=0,
解得k=5.
故选:D.
| a |
| b |
| a |
| b |
| b |
∴(k
| a |
| b |
| b |
解得k=5.
故选:D.
点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意向量垂直的性质的合理运用.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
在复平面内,复数(1-2i)2的共轭复数对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
不等式2x-3<1的解集是( )
| A、(-∞,2] |
| B、(-∞,2) |
| C、(2,+∞) |
| D、[-∞,2) |
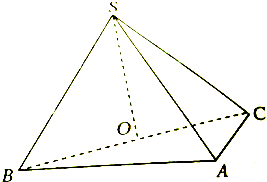 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.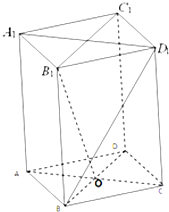 如图,四棱柱中A1B1C1D1-ABCD,底面ABCD为边长为2的菱形,侧棱长为3,且∠B1BA=∠B1BC=∠ABC=60°.
如图,四棱柱中A1B1C1D1-ABCD,底面ABCD为边长为2的菱形,侧棱长为3,且∠B1BA=∠B1BC=∠ABC=60°. 如图ABCD是菱形,PA⊥平面ABCD,E、F分别是PC、AB的中点.
如图ABCD是菱形,PA⊥平面ABCD,E、F分别是PC、AB的中点.