题目内容
解下列不等式:
(1)2x2+5x-3>0
(2)
≥2.
(1)2x2+5x-3>0
(2)
| x-1 |
| x+3 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:根据不等式的解法进行求解即可.
解答:
解:(1)由2x2+5x-3>0,
得(x+3)(2x-1)>0,
解得x>
或x<-3,
即不等式的解集为{x|x>
或x<-3}.
(2)由
≥2得
-2=
≥0,
即
≤0,
解得-7≤x<-3,
故不等式的解集为[-7,-3).
得(x+3)(2x-1)>0,
解得x>
| 1 |
| 2 |
即不等式的解集为{x|x>
| 1 |
| 2 |
(2)由
| x-1 |
| x+3 |
| x-1 |
| x+3 |
| -x-7 |
| x+3 |
即
| x+7 |
| x+3 |
解得-7≤x<-3,
故不等式的解集为[-7,-3).
点评:本题主要考查不等式的求解,要求熟练掌握各种不等式的解法.

练习册系列答案
相关题目
不等式2x-3<1的解集是( )
| A、(-∞,2] |
| B、(-∞,2) |
| C、(2,+∞) |
| D、[-∞,2) |
设a,b是非零实数,若a<b,则下列不等式成立的是( )
| A、a2<b2 | ||||
B、
| ||||
| C、2a<2b | ||||
D、
|

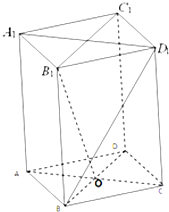 如图,四棱柱中A1B1C1D1-ABCD,底面ABCD为边长为2的菱形,侧棱长为3,且∠B1BA=∠B1BC=∠ABC=60°.
如图,四棱柱中A1B1C1D1-ABCD,底面ABCD为边长为2的菱形,侧棱长为3,且∠B1BA=∠B1BC=∠ABC=60°.