题目内容
在△ABC中，AB、AC边的长分别是2和1，∠A=60°，若AD平分∠BAC交BC于D，则
•
= ．
| AD |
| BD |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由于AB、AC边的长分别是2和1，∠A=60°，利用余弦定理可得a2=b2+c2-2bccosA=3．利用角平分线的性质可得
=
=
，BD．在△ABD中，由余弦定理可得：BD2=AB2+AD2-2AB•ADcos30°，解得AD=
．再利用数量积定义
•
即可得出．
| BD |
| DC |
| AB |
| AC |
| 2 |
| 1 |
2
| ||
| 3 |
| AD |
| BD |
解答：
解：∵AB、AC边的长分别是2和1，∠A=60°，
∴a2=b2+c2-2bccosA=22+12-2×2×1cos60°=3．
∴a=
．
∵
=
=
，
∴BD=
，
在△ABD中，由余弦定理可得：BD2=AB2+AD2-2AB•ADcos30°，
(
)2=22+AD2-2
AD，
解得AD=
．
∴∠B=30°．
∴∠ADB=150°．
∴
•
=|
||
|cos150°
=(
)2×(-
)
=-
．
故答案为：-
．
∴a2=b2+c2-2bccosA=22+12-2×2×1cos60°=3．
∴a=
| 3 |
∵
| BD |
| DC |
| AB |
| AC |
| 2 |
| 1 |
∴BD=
2
| ||
| 3 |
在△ABD中，由余弦定理可得：BD2=AB2+AD2-2AB•ADcos30°，
(
2
| ||
| 3 |
| 3 |
解得AD=
2
| ||
| 3 |
∴∠B=30°．
∴∠ADB=150°．
∴
| AD |
| BD |
| AD |
| BD |
=(
2
| ||
| 3 |
| ||
| 2 |
=-
2
| ||
| 3 |
故答案为：-
2
| ||
| 3 |
点评：本题考查了角平分线的性质、余弦定理、数量积定义，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=
（e为自然对数的底数），已知函数g（x）=f（x）-m有两个零点，则实数m的取值范围为（ ）
|
| A、0＜m＜1 | B、0＜m≤1 |
| C、m＞1 | D、m≥1 |
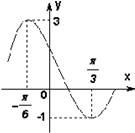已知三角函数f（x）=Acos（ωx+φ）+b（A＞ω＞0，|φ|＜