题目内容
18．若直线ax+by=2与圆x2+y2=1有公共点，则（ ）| A． | a2+b2≤4 | B． | a2+b2≥4 | C． | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≤4 | D． | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≥4 |
分析 根据直线ax+by=2和圆x2+y2=1有公共点，通过圆心到直线的距离小于等于半径，即可推出a，b关系．
解答 解：因为直线ax+by=2和圆x2+y2=1有公共点，
所以圆心到直线ax+by-2=0的距离d=$\frac{2}{\sqrt{{a}^{2}+{b}^{2}}}$≤1，
解得a2+b2≥4，
故选：B．
点评 本题主要考查了直线与圆的位置关系，考查计算能力．
练习册系列答案
相关题目
20．函数y=cos（$\frac{π}{2}$-x）sin（$\frac{π}{2}$+x）的最小正周期为（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{3π}{2}$ | D． | 2π |
6．下列命题中的真命题是（ ）
| A． | ?x0∈R，使得x0+$\frac{1}{x0}$=$\frac{3}{2}$ | B． | ?x∈（0，+∞），ex＞x+1 | ||
| C． | ?x0∈R，使得x${\;}_{{0}^{\;}}$2-x0+1=0 | D． | ?x∈（0，π），sinx＞cosx |
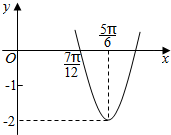函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）在区间[0，$\frac{π}{2}$]上的最小值为-1．
8．执行如图所示的程序框图，若p=0.9，则输出的n为（ ）
| A． | 6 | B． | 5 | C． | 4 | D． | 3 |