题目内容
6.为了对某课题进行研究,用分层抽样的方法从三所高校A,B,C的相关人中抽取若干人组成研究小组,有关数据如下表(单位:人).| 高校 | 相关人数 | 抽取人数 |
| A | 54 | x |
| B | 36 | 2 |
| C | 72 | y |
(2)若从高校B,C抽取的人中选2人作专题发言,求这2人均来自高校C的概率.
分析 (1)由分层抽样的性质求解.
(2)从高校B,C抽取的人中选2人作专题发言,先求出基本事件总,再求出这2人均来自高校C包含的基本事件个数,由此能求出这2人均来自高校C的概率.
解答 解:(1)由分层抽样的性质得:
$\frac{x}{54}=\frac{2}{36}=\frac{y}{72}$,
解得x=3,y=4.
(2)从高校B,C抽取的人中选2人作专题发言,
基本事件总数n=${C}_{6}^{2}$=15,
这2人均来自高校C包含的基本事件个数m=${C}_{4}^{2}$=6,
∴这2人均来自高校C的概率p=$\frac{m}{n}$=$\frac{6}{15}$=$\frac{2}{5}$.
点评 本题考查分层抽样的性质的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
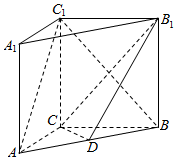 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.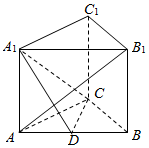 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.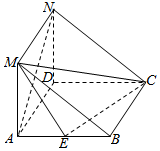 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.