题目内容
16.f(x)=$\frac{1}{2}$cos(2x+$\frac{π}{6}$)+$\frac{1}{4}$.①求f(x)的单调区间;
②若x∈[0,$\frac{π}{2}$],求f(x)的值域.
分析 ①根据余弦函数的单调性列出不等式解出f(x)的单调区间.
②根据x的范围求出2x+$\frac{π}{6}$的范围,根据余弦函数的图象和单调性得出f(x)的最值.
解答 解:①令-π+2kπ≤2x+$\frac{π}{6}$≤2kπ,解得-$\frac{7π}{12}$+kπ≤x≤-$\frac{π}{12}$+kπ,
令2kπ≤2x+$\frac{π}{6}$≤π+2kπ,解得-$\frac{π}{12}+kπ$≤x≤$\frac{5π}{12}+kπ$.
∴f(x)的增区间是[-$\frac{7π}{12}$+kπ,-$\frac{π}{12}$+kπ],减区间是[-$\frac{π}{12}+kπ$,$\frac{5π}{12}+kπ$],k∈Z.
②∵x∈[0,$\frac{π}{2}$],∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$].
∴当2x+$\frac{π}{6}$=$\frac{π}{6}$时,f(x)取得最大值$\frac{1}{2}×\frac{\sqrt{3}}{2}+\frac{1}{4}$=$\frac{\sqrt{3}+1}{4}$,
当2x+$\frac{π}{6}$=π时,f(x)取得最小值$\frac{1}{2}×(-1)$$+\frac{1}{4}$=-$\frac{1}{4}$.
∴f(x)的值域是[-$\frac{1}{4}$,$\frac{\sqrt{3}+1}{4}$].
点评 本题考查了余弦函数的图象与性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列函数中,与函数y=x+1是同一个函数的是( )
| A. | $y={(\sqrt{x+1})^2}$ | B. | $y=\root{3}{x^3}+1$ | C. | $y=\frac{x^2}{x}+1$ | D. | $y=\sqrt{x^2}+1$ |
4.已知△ABC,P为三角形所在平面上的一点,且点P满足:a$•\overrightarrow{PA}$+b$•\overrightarrow{PB}$+c$•\overrightarrow{PC}$=0,则P点为三角形( )
| A. | 外心 | B. | 内心 | C. | 重心 | D. | 垂心 |
5.若直线l1:(a+1)x+a2y-3=0与直线l:2x+ay-2a-1=0平行,则a=( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | 0或-1 |
8.下列说法错误的是( )
| A. | 命题p:“?x0∈R,x02+x0+1<0”,则¬p:“?x∈R,x2+x+1≥0” | |
| B. | 命题“若x2-4x+3=0,则x=3”的逆否命题是假命题 | |
| C. | 命题“若m>0,则方程x2+x-m=0有实数根”的否定是“若m>0,则方程x2+x-m=0没有实数根” | |
| D. | 若p∧q为假命题,则p∨q为假命题 |
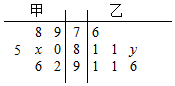 高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.