题目内容
已知函数f(x)=x3-
x2+bx+c.
(1)若f(x)有极值,求b的取值范围;
(2)若f(x)在x=1处取得极值,当x∈[-1,2]时,则f(x)<c2恒成立,求c的取值范围.
| 1 |
| 2 |
(1)若f(x)有极值,求b的取值范围;
(2)若f(x)在x=1处取得极值,当x∈[-1,2]时,则f(x)<c2恒成立,求c的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)f′(x)=3x2-x+b.f(x)有极值?f′(x)=0由两个不相等的实数根?△=1-12b>0,解得即可.
(2)当x∈[-1,2]时,则f(x)<c2恒成立?f(x)max<c2,利用导数求出f(x)max即可解出.
(2)当x∈[-1,2]时,则f(x)<c2恒成立?f(x)max<c2,利用导数求出f(x)max即可解出.
解答:
解:(1)f′(x)=3x2-x+b.令f′(x)=0,
由△=1-12b>0,解得b<
.
(2)∵f(x)在x=1处取得极值,
∴f′(1)=0,∴3-1+b=0,得b=-2.
∴f′(x)=3x2-x-2.
令f′(x)=0,得x1=-
,x2=1.
列表如下:
由表格可知:当x=-
时,函数f(x)取得极大值f(-
)=
+c,而区间端点处的f(2)=2+c,
∴函数f(x)的最大值为2+c.
∴2+c<c2,解得c>2或c<-1.
∴c的取值范围是c>2或c<-1.
由△=1-12b>0,解得b<
| 1 |
| 12 |
(2)∵f(x)在x=1处取得极值,
∴f′(1)=0,∴3-1+b=0,得b=-2.
∴f′(x)=3x2-x-2.
令f′(x)=0,得x1=-
| 2 |
| 3 |
列表如下:
| x | [-1,-
| -
| (-
| 1 | (1,2] | ||||||
| f′(x) | + | 0 | - | 0 | + | ||||||
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
| 2 |
| 3 |
| 2 |
| 3 |
| 22 |
| 27 |
∴函数f(x)的最大值为2+c.
∴2+c<c2,解得c>2或c<-1.
∴c的取值范围是c>2或c<-1.
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
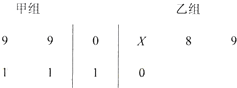 以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.