Question

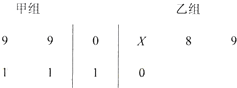以下茎叶图记录了甲、乙两组各四名同学的植树棵数．乙组记录中有一个数据模糊，无法确认，在图中以X表示．
（1）如果X=8，求乙组同学植树棵数的平均数和方差；
（2）如果X=9，求乙组同学植树棵数的中位数和众数；
（3）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数Y的分布列和数学期望．

Answer 1

考点：离散型随机变量的期望与方差,茎叶图,离散型随机变量及其分布列

专题：概率与统计

分析：（1）当X=8时，利用茎叶图能求出乙组同学植树棵数的平均数和方差．
（2）当X=9时，利用茎叶图能求出乙组同学植树棵数的中位数和众数．
（3）当X=9时，由茎叶图可知，甲组同学的植树棵树是：9，9，11，11；乙组同学的植树棵数是：9，8，9，10．这两名同学植树总棵数Y的可能取值为17，18，19，20，21，分别求出相应的概率，由此能求出这两名同学的植树总棵数Y的分布列和数学期望．

解答： 解：（1）当X=8时，由茎叶图可知，乙组同学的植树棵数是：8，8，9，10，
所以平均数为

x

=

8+8+9+10

4

=

35

4

；…（1分）
方差为

s

2

=

1

4

[(8-

35

4

)

2

+(9-

35

4

)

2

+(10-

35

4

)

2

]=

11

16

．…（2分）
（2）当X=9时，由茎叶图可知，乙组同学的植树棵数是：8，9，9，10．
中位数9，众数9．…（4分）
（3）当X=9时，由茎叶图可知，
甲组同学的植树棵树是：9，9，11，11；
乙组同学的植树棵数是：9，8，9，10．
分别从甲、乙两组中随机选取一名同学，共有4×4=16种可能的结果，
这两名同学植树总棵数Y的可能取值为17，18，19，20，21，
事件“Y=17”等价于“甲组选出的同学植树9棵，
乙组选出的同学植树8棵”所以该事件有2种可能的结果，
因此P（Y=17）=

2

16

=

1

8

．
同理可得P（Y=18）=

1

4

，P（Y=19）=

1

4

，
P（Y=20）=

1

4

，P（Y=21）=

1

8

，
所以随机变量Y的分布列为：

Y	17	18	19	20	21
P	1 8	1 4	1 4	1 4	1 8

EY=17×P（Y=17）+18×P（Y=18）+19×P（Y=19）+20×P（Y=20）+21×P（Y=21）=17×

1

8

+18×

1

4

+19×

1

4

+20×

1

4

+21×

1

8

=19．…（10分）

点评：本题考查平均数、方差、中位数、众数的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要注意茎叶图的合理运用．