题目内容
 已知三棱锥P-ABC的底面ABC是直角三角形,且∠ACB=90°,PA⊥平面ABC,PA=AC=BC=1,D是线段PC的中点,如图所示.
已知三棱锥P-ABC的底面ABC是直角三角形,且∠ACB=90°,PA⊥平面ABC,PA=AC=BC=1,D是线段PC的中点,如图所示.(Ⅰ)证明:AD⊥平面PBC;
(Ⅱ)求三棱锥P-ABD的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)只要证明AD由于面PBC内的PC,BC垂直即可;
(Ⅱ)利用∴D到面PAB的距离等于C到面PAB的距离的一半,将三棱锥P-ABD的体积利用三棱锥C-PAB的体积的一半表示.
(Ⅱ)利用∴D到面PAB的距离等于C到面PAB的距离的一半,将三棱锥P-ABD的体积利用三棱锥C-PAB的体积的一半表示.
解答:
证明:(Ⅰ)∵PA=AC,D是线段PC的中点,
∴AD⊥PC,
∵BC⊥AC,BC⊥PA,
∴BC⊥面PAC,
∴BC⊥AD,
∴AD⊥面PBC;
(Ⅱ)∵点D是PC的中点,
∴D到面PAB的距离等于C到面PAB的距离的一半,
∴VP-ABD=VD-PAB=
VC-PAB,
又VC-PAB=VP-ABC=
S△ABC×PA=
×
AC×BC=
PA×
=
,
∴VP-ABD=
.
∴AD⊥PC,
∵BC⊥AC,BC⊥PA,
∴BC⊥面PAC,
∴BC⊥AD,
∴AD⊥面PBC;
(Ⅱ)∵点D是PC的中点,
∴D到面PAB的距离等于C到面PAB的距离的一半,
∴VP-ABD=VD-PAB=
| 1 |
| 2 |
又VC-PAB=VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
∴VP-ABD=
| 1 |
| 12 |
点评:本题考查了线面垂直的判定 以及三棱锥体积的求法,注意将体积转化,使计算简便.

练习册系列答案
相关题目
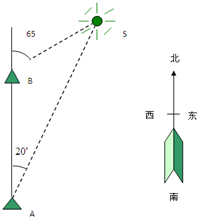 如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?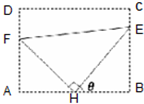 如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10
如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10