题目内容
7.已知圆O:x2+y2=1,点P(-1,2),过点P作圆O的切线,求切线方程.分析 当过点(-1,2)的直线斜率不存在时,方程是x=-1,通过验证圆心到直线的距离,得到x=-1符合题意;当过点(-1,2)的直线斜率存在时,设直线方程为y-2=k(x+1),根据圆心到直线的距离等于半径1,建立关于k的方程,即可得出结论.
解答 解:圆x2+y2=1的圆心为原点,半径为1
(1)当过点(-1,2)的直线垂直于x轴时,此时直线斜率不存在,方程是x=-1,
因为圆心O(0,0)到直线的距离为d=1=r,所以直线x=-1符合题意;
(2)当过点(-1,2)的直线不垂直于x轴时,设直线方程为y-2=k(x+1),即kx-y+k+2=0
∵直线是圆x2+y2=1的切线
∴点O到直线的距离为d=$\frac{|k+2|}{\sqrt{{k}^{2}+1}}$=1,解之得k=-$\frac{3}{4}$,
此时直线方程为3x+4y-5=0
综上所述,得切线方程为切线方程为3x+4y-5=0或x=-1.
点评 本题考查了直线与圆的位置关系、点到直线的距离公式等知识点,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
15.定义在R上的奇函数f(x),当x∈(-∞,0)时xf(x)递减,若a=3f(3),b=(logπ3)•f(logπ3),c=-2f(-2),则a,b,c的大小关系( )
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | b<c<a |
2.某校高一学生1500人,高二学生1200人,高三学生1300人,为了调查高中各年级学生的寒假学习计划,决定采用分层抽样法抽取200人进行调查,则应从高二年级抽取的人数为( )
| A. | 75 | B. | 65 | C. | 60 | D. | 40 |
12.设p:“$\frac{a-1}{a-2}$≥0”,q:“圆x2+y2=a2(a>0)与直线3x+4y-5=0相交且与圆(x+3)2+(y+4)2=9外离”,则¬p是q的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
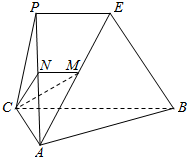 如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.
如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.