题目内容
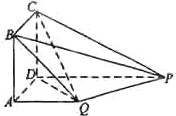 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=| 1 |
| 2 |
(Ⅰ)证明:平面PQC⊥平面DCQ;
(Ⅱ)求平面QBP与平面BPC的夹角余弦值.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(Ⅰ)根据已知条件建立空间直角坐标系,求向量
,
,
的坐标,求
•
,
•
,从而判断出
⊥
,
⊥
,这样即可证明PQ⊥平面DCQ,这样便可证明平面PQC⊥平面DCQ;
(Ⅱ)根据平面的法向量和平面内两向量垂直,求出平面BPC和平面QBP的法向量,根据这两法向量的夹角的余弦值求出这两平面夹角的余弦值.
| CD |
| DQ |
| PQ |
| PQ |
| CD |
| PQ |
| DQ |
| PQ |
| CD |
| PQ |
| DQ |
(Ⅱ)根据平面的法向量和平面内两向量垂直,求出平面BPC和平面QBP的法向量,根据这两法向量的夹角的余弦值求出这两平面夹角的余弦值.
解答:
解:(Ⅰ)证明:由已知条件知,DA,DP,DC三条直线两两垂直,∴如图,分别以DA,DP,DC所在直线为x轴,y轴,z轴建立D-xyz空间直角坐标系,则可确定以下几点坐标: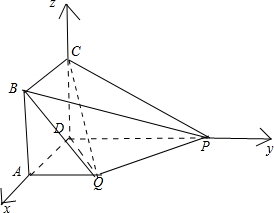 Q(1,1,0),C(0,0,1),P(0,2,0),D(0,0,0);
Q(1,1,0),C(0,0,1),P(0,2,0),D(0,0,0);
∴
=(1,1,0),
=(0,0,1),
=(1,-1,0);
∴
•
=0,
•
=0,∴
⊥
,
⊥
即PQ⊥DQ,PQ⊥DC,DQ∩DC=D;
∴PQ⊥平面DCQ,又PQ?平面PQC;
∴平面PQC⊥平面DCQ;
(Ⅱ)依题意知:B(1,0,1),∴
=(1,0,0),
=(-1,2,-1);
设
=(x,y,z)是平面BPC的法向量,则
,即
,解得
;
∴可取
=(0,1,2);
同样,设
=(x,y,z)是平面QBP的法向量,则:
,即
,解得
;
∴取
=(1,1,1);
∴设平面QBP与平面BPC的夹角为θ,则cosθ=
=
=
.
 Q(1,1,0),C(0,0,1),P(0,2,0),D(0,0,0);
Q(1,1,0),C(0,0,1),P(0,2,0),D(0,0,0);∴
| DQ |
| DC |
| PQ |
∴
| PQ |
| DQ |
| PQ |
| DC |
| PQ |
| DQ |
| PQ |
| DC |
∴PQ⊥平面DCQ,又PQ?平面PQC;
∴平面PQC⊥平面DCQ;
(Ⅱ)依题意知:B(1,0,1),∴
| CB |
| BP |
设
| n |
|
|
|
∴可取
| n |
同样,设
| m |
|
|
|
∴取
| m |
∴设平面QBP与平面BPC的夹角为θ,则cosθ=
| ||||
|
|
| 3 | ||||
|
| ||
| 5 |
点评:考查建立空间直角坐标系,用向量的方法证明面面垂直,求两平面夹角的方法,向量的数量积,及向量垂直的充要条件,平面法向量的概念,线面垂直的判定定理,面面垂直的判定定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
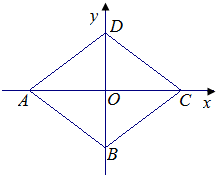 如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒.
如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒.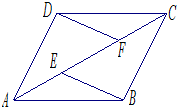 如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形.
如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形. 用红黄蓝三种颜色给如图所示的六连圆涂色,若每种颜色只能涂两个圆,且相邻两个圆所涂颜色不能相同,则不同的涂色方案共有
用红黄蓝三种颜色给如图所示的六连圆涂色,若每种颜色只能涂两个圆,且相邻两个圆所涂颜色不能相同,则不同的涂色方案共有