题目内容
16.从3男2女共5名学生中任选2人参加座谈会,则选出的2人恰好为1男1女的概率为$\frac{3}{5}$.分析 先求出基本事件总数n=${C}_{5}^{2}$=10,再求出选出的2人恰好为1男1女包含的基本事件个数m=${C}_{3}^{1}{C}_{2}^{1}=6$,由此能求出选出的2人恰好为1男1女的概率.
解答 解:从3男2女共5名学生中任选2人参加座谈会,
基本事件总数n=${C}_{5}^{2}$=10,
选出的2人恰好为1男1女包含的基本事件个数m=${C}_{3}^{1}{C}_{2}^{1}=6$,
∴选出的2人恰好为1男1女的概率p=$\frac{m}{n}$=$\frac{6}{10}=\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
11.手机完全充满电量,在开机不使用的状态下,电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间.为了解A,B两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取A,B两个型号的手机各5台,在相同条件下进行测试,统计结果如下:
已知 A,B两个型号被测试手机待机时间的平均值相等.
(Ⅰ)求a的值;
(Ⅱ)判断A,B两个型号被测试手机待机时间方差的大小(结论不要求证明);
(Ⅲ)从被测试的手机中随机抽取A,B型号手机各1台,求至少有1台的待机时间超过122小时的概率.
(注:n个数据x1,x2,…,xn的方差s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$为数据x1,x2,…,xn的平均数)
| 手机编号 | 1 | 2 | 3 | 4 | 5 |
| A型待机时间(h) | 120 | 125 | 122 | 124 | 124 |
| B型待机时间(h) | 118 | 123 | 127 | 120 | a |
(Ⅰ)求a的值;
(Ⅱ)判断A,B两个型号被测试手机待机时间方差的大小(结论不要求证明);
(Ⅲ)从被测试的手机中随机抽取A,B型号手机各1台,求至少有1台的待机时间超过122小时的概率.
(注:n个数据x1,x2,…,xn的方差s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$为数据x1,x2,…,xn的平均数)
5.设函数f(x)=cosx+2sinx,则f′($\frac{π}{4}$)=( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
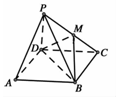 已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上
已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上