题目内容
已知x＞-2，求函数y=x+
的最小值．
| 1 |
| x+2 |
考点：基本不等式
专题：计算题,不等式的解法及应用
分析：y=x+
=x+2+
-2，利用基本不等式即可求得函数的最小值，注意等号取到的条件．
| 1 |
| x+2 |
| 1 |
| x+2 |
解答：
解：∵x＞-2，
∴y=x+
=x+2+
-2≥2
-2=0，
当且仅当x+2=
，即x=-1时取等号，
∴x=-1时，函数y=x+
取最小值0．
∴y=x+
| 1 |
| x+2 |
| 1 |
| x+2 |
(x+2)•
|
当且仅当x+2=
| 1 |
| x+2 |
∴x=-1时，函数y=x+
| 1 |
| x+2 |
点评：该题考查利用基本不等式求函数的最值，属基础题，注意使用基本不等式的条件：一正、二定、三相等．
练习册系列答案
考前必练系列答案
相关题目
将最小正周期为3π的函数f（x）=cos（ωx+φ）-sin（ωx+φ）（ω＞0，|φ|＜
）的图象向左平移
个单位，得到偶函数图象，则满足题意的φ的一个可能值为（ ）
| π |
| 2 |
| π |
| 4 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
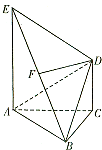如图，AE⊥平面ABC，CD∥AE，F是BE的中点，已知AC=BC=CD=1，AE=2，∠ACB=90°．
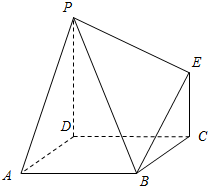如图，简单组合体ABCDPE，其底面ABCD是边长为2的正方形，PD⊥平面ABCD，EC∥PD，且PD=2EC=2．