题目内容
复数z=1+
的模为 .
| 1 |
| i |
考点:复数求模
专题:数系的扩充和复数
分析:化简复数为a+bi的形式,然后求模即可.
解答:
解:复数z=1+
=1+
=1-i.
复数z=1+
的模为:
=
故答案为:
.
| 1 |
| i |
| i |
| i•i |
复数z=1+
| 1 |
| i |
| 1+(-1)2 |
| 2 |
故答案为:
| 2 |
点评:本题考查复数代数形式的混合运算,复数模的求法,考查计算能力.

练习册系列答案
相关题目
对于R上可导的任意函数f(x),若满足(2-x)f′(x)≤0,则必有( )
| A、f(1)+f(3)<2f(2) |
| B、f(1)+f(3)≤2f(2) |
| C、f(1)+f(3)>2f(2) |
| D、f(1)+f(3)≥2f(2) |
圆心在直线y=2x上,半径为
且与直线2x+y+1=0相切的圆的方程为( )
| 5 |
| A、(x-2)2+(y-1)2=5 |
| B、(x-1)2+(y-2)2=5 |
| C、(x-2)2+(y-1)2=25 |
| D、(x-1)2+(y-2)2=25 |
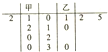 2014年1月8日是传统的腊八节,大家开始购买年货,某淘宝网店趁势推出“抢红包”的促销活动,已知每人有5次抢红包的机会,每次可得1至30元不等的红包,甲、乙二人在这5次抢红包活动中获得红包金额的茎叶图如图所示,若甲5次获得红包金额的均值为
2014年1月8日是传统的腊八节,大家开始购买年货,某淘宝网店趁势推出“抢红包”的促销活动,已知每人有5次抢红包的机会,每次可得1至30元不等的红包,甲、乙二人在这5次抢红包活动中获得红包金额的茎叶图如图所示,若甲5次获得红包金额的均值为