题目内容
15.已知a、b、c三个实数成等差数列,则直线bx+ay+c=0与抛物线${y^2}=-\frac{1}{2}x$的相交弦中点的轨迹方程是x+1=-(2y-1)2(y≠1)..分析 联立方程组,用交点坐标表示出中点坐标,代入直线方程化简即可.
解答 解:设直线bx+ay+c=0与抛物线${y^2}=-\frac{1}{2}x$的交点坐标为A(-2y12,y1),B(-2y22,y2),
把x=-2y2代入直线方程bx+ay+c=0得:-2by2+ay+c=0,
∴y1y2=$\frac{c}{-2b}$,y1+y2=$\frac{a}{2b}$,
∵a,b,c成等差数列,∴c=2b-a,
∴y1y2=$\frac{2b-a}{-2b}$=$\frac{a}{2b}$-1,
设AB的中点为P(x,y),则x=-y12-y22=-(y1+y2)2+2y1y2=-$\frac{{a}^{2}}{4{b}^{2}}$+$\frac{a}{b}$-2,
y=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{a}{4b}$,
∴x=-4y2+4y-2,即x+1=-(2y-1)2,
由△=a2+8bc=a2+8b(2b-a)=a2-8ab+16b2=(a-4b)2>0得a≠4b,
∴y≠1.
故答案为:x+1=-(2y-1)2(y≠1).
点评 本题考查了轨迹方程的求解,根与系数的关系,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
3.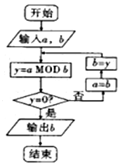 如图的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为485,270,则输出的b=( )
如图的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为485,270,则输出的b=( )
 如图的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为485,270,则输出的b=( )
如图的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为485,270,则输出的b=( )| A. | 0 | B. | 10 | C. | 5 | D. | 55 |
7.若复数z=1+i,$\overline z$为z的共轭复数,则z•$\overline z$=( )
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 2i |
4.已知函数$f(x)=sin\frac{πx}{6}$,集合M={0,1,2,3,4,5,6,7,8},现从M中任取两个不同元素m,n,则f(m)f(n)=0的概率为( )
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{7}{18}$ | D. | $\frac{7}{9}$ |
18.证明$\frac{n+2}{2}<1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+…+\frac{1}{2^n}<n+1(n>1)$,当n=2时,中间式子等于( )
| A. | 1 | B. | $1+\frac{1}{2}$ | C. | $1+\frac{1}{2}+\frac{1}{3}$ | D. | $1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ |