题目内容
18.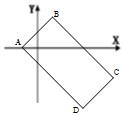 如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.
如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.(Ⅰ)求D点对应的复数;
(Ⅱ)求平行四边形ABCD的面积.
分析 (I)利用复数的几何意义、向量的坐标运算性质、平行四边形的性质即可得出.
(II)利用向量垂直与数量积的关系、模的计算公式、矩形的面积计算公式即可得出.
解答 解:(Ⅰ)依题点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,
得A(-1,0),$\overrightarrow{AB}$=(2,2),可得B(1,2).
又$\overrightarrow{BC}$对应的复数为4-4i,得$\overrightarrow{BC}$=(4,-4),可得C(5,-2).
设D点对应的复数为x+yi,x,y∈R.
得$\overrightarrow{CD}$=(x-5,y+2),$\overrightarrow{BA}$=(-2,-2).
∵ABCD 为平行四边形,∴$\overrightarrow{BA}$=$\overrightarrow{CD}$,解得x=3,y=-4,
故D点对应的复数为3-4i.
(Ⅱ)$\overrightarrow{AB}$=(2,2),$\overrightarrow{BC}$=(4,-4),
可得:$\overrightarrow{AB}•\overrightarrow{BC}$=0,∴$\overrightarrow{AB}$$⊥\overrightarrow{BC}$.
又|$\overrightarrow{AB}$|=2$\sqrt{2}$,$|\overrightarrow{BC}|$=4$\sqrt{2}$.
故平行四边形ABCD的面积=$2\sqrt{2}×4\sqrt{2}$=16.
点评 本题考查了复数的几何意义、向量的坐标运算性质、平行四边形的性质、向量垂直与数量积的关系、模的计算公式、矩形的面积计算公式,考查了推理能力与计算能力,属于中档题.

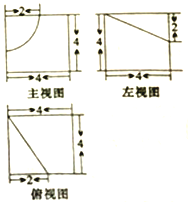
| A. | 64 | B. | 64-4π | C. | 64-8π | D. | 64-$\frac{4π}{3}$ |
| A. | 0 | B. | 1 | C. | -a | D. | 不确定 |
| A. | $\frac{1}{2n+1}+\frac{1}{2n+2}$ | B. | $\frac{1}{2n+2}-\frac{1}{n+1}$ | ||
| C. | $\frac{1}{2n+2}$ | D. | $\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}$ |
| 分组(身高) | [125,130) | [130,135) | [135,140) | [140,145] |
(Ⅱ)在(Ⅰ)中抽取的6人中,再随机抽取2人,求这2人身高都在[125,130)内的概率.
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |